题目内容
已知非零向量 、
、 若|
若| |=|
|=| |=1,且a⊥b,又知(k
|=1,且a⊥b,又知(k -4
-4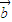 )⊥(2
)⊥(2 +3
+3 ),则实数k的值为( )
),则实数k的值为( )A.6
B.3
C.-3
D.-6
【答案】分析:根据向量垂直则数量积为0,所以(k -4
-4 )(2
)(2 +3
+3 )=0;展开运算可得k值.
)=0;展开运算可得k值.
解答:解:因为向量(k -4
-4 )和(2
)和(2 +3
+3 )垂直,所以(k
)垂直,所以(k -4
-4 )(2
)(2 +3
+3 )=0,
)=0,
(k -4
-4 )(2
)(2 +3
+3 )=2k
)=2k 2+3k
2+3k
 -8
-8 b-12
b-12 2注意到条件|
2注意到条件| |=|
|=| |=1,
|=1,
则 2|=|
2|=| |2=1,
|2=1, 2=|
2=| |2=1;
|2=1;
而 垂直于
垂直于 ,所以
,所以
 =0;
=0;
所以,2k-12=0,k=6;
故答案为6.
点评:本题考查向量垂直于数量积关系
 -4
-4 )(2
)(2 +3
+3 )=0;展开运算可得k值.
)=0;展开运算可得k值.解答:解:因为向量(k
 -4
-4 )和(2
)和(2 +3
+3 )垂直,所以(k
)垂直,所以(k -4
-4 )(2
)(2 +3
+3 )=0,
)=0,(k
 -4
-4 )(2
)(2 +3
+3 )=2k
)=2k 2+3k
2+3k
 -8
-8 b-12
b-12 2注意到条件|
2注意到条件| |=|
|=| |=1,
|=1,则
 2|=|
2|=| |2=1,
|2=1, 2=|
2=| |2=1;
|2=1;而
 垂直于
垂直于 ,所以
,所以
 =0;
=0;所以,2k-12=0,k=6;
故答案为6.
点评:本题考查向量垂直于数量积关系

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,若
,若 与
与 互相垂直,则
互相垂直,则
 B.
B. C.
C. D.
D.
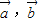 ,若|
,若| |=|
|=| |=1,且
|=1,且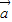 ⊥
⊥ ,又知(2
,又知(2 +3
+3 )⊥(k
)⊥(k -4
-4 ),则实数k的值为( )
),则实数k的值为( ) ,若|
,若| |=|
|=| |=1,且
|=1,且 ⊥
⊥ ,又知(2
,又知(2 +3
+3 )⊥(k
)⊥(k -4
-4 ),则实数k的值为( )
),则实数k的值为( ) 、
、 若|
若| |=|
|=|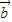 |=1,且a⊥b,又知(k
|=1,且a⊥b,又知(k -4
-4 )⊥(2
)⊥(2 +3
+3 ),则实数k的值为( )
),则实数k的值为( )