题目内容
设数列 是各项均为正数的等比数列,其前项和为
是各项均为正数的等比数列,其前项和为 ,若
,若 ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)对于正整数 ),求证:“
),求证:“ 且
且 ”是“
”是“ 这三项经适当排序后能构成等差数列”成立的充要条件;
这三项经适当排序后能构成等差数列”成立的充要条件;
(3)设数列 满足:对任意的正整数,都有
满足:对任意的正整数,都有 ,且集合
,且集合 中有且仅有3个元素,试求的取值范围.
中有且仅有3个元素,试求的取值范围.
解:(1) 数列
数列 是各项均为正数的等比数列,
是各项均为正数的等比数列,
 ,
, ,
,
又
 ,
, ,
, ,
, ;
;
(2)(ⅰ)必要性:设 这三项经适当排序后能构成等差数列,
这三项经适当排序后能构成等差数列,
①若 ,则
,则 ,
, ,
, ,
,

 . ②若
. ②若 ,则
,则 ,
, ,左边为偶数,等式不成立,
,左边为偶数,等式不成立,
③若 ,同理也不成立,
,同理也不成立,
综合①②③,得 ,所以必要性成立.
,所以必要性成立.
(ⅱ)充分性:设 ,
, ,
,
则 这三项为
这三项为 ,即
,即 ,调整顺序后易知
,调整顺序后易知 成等差数列,所以充分性也成立.
成等差数列,所以充分性也成立.
综合(ⅰ)(ⅱ),原命题成立.
(3)因为 ,
,
即 ,(*)
,(*)
 当
当 时,
时, ,(**)
,(**)
则(**)式两边同乘以2,得 ,(***)
,(***)
 (*)-(***),得
(*)-(***),得 ,即
,即 ,
,
又当 时,
时, ,即
,即 ,适合
,适合 ,
,
 ,
, ,
,
 时,
时, ,即
,即 ;
;
 时,
时, ,此时
,此时 单调递减,
单调递减,
又 ,
, ,
, ,
, ,
, .
.

练习册系列答案
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案
相关题目
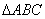 中,三内角
中,三内角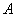 ,
,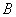 ,
,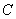 的对边分别为
的对边分别为 ,
,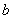 ,
, 且
且 ,
, ,
, 为
为 的最大值为 .
的最大值为 . 与圆
与圆 的公共弦的长为8,则
的公共弦的长为8,则 ___________.
___________. (其中
(其中 为整数),则
为整数),则 ,即
,即 . 在此基础上给出下列关于函数
. 在此基础上给出下列关于函数 的四个命题:
的四个命题: 的定义域是R,值域是
的定义域是R,值域是 ;
; 是
是 ;
; 上是增函数.
上是增函数. ,
, ,
, ,则
,则 的大小关系是( )
的大小关系是( )  B.
B. C.
C. D.
D.
 是双曲线
是双曲线 的左、右焦点,过
的左、右焦点,过 且垂直于
且垂直于 轴的直线与双曲线交于
轴的直线与双曲线交于 两点,若
两点,若 为钝角三角形,则该双曲线的离心率
为钝角三角形,则该双曲线的离心率 的取值范围是( )
的取值范围是( ) B.
B.
 D.
D.
 ;
; ;
;
 B.
B. C.
C.  D.6
D.6