题目内容
已知向量
=(x1,y1),
=(x2,y2),
=(1,0),若
≠
,|
-
|=R,且
-
与
夹角为
,则x1-x2等于( )
| a |
| b |
| e |
| a |
| b |
| a |
| b |
| a |
| b |
| e |
| π |
| 3 |
| A、R | ||||
B、
| ||||
C、
| ||||
D、
|
分析:由向量
=(x1,y1),
=(x2,y2),求出
-
,根据数量积的定义和数量积的坐标运算,求得x1-x2.
| a |
| b |
| a |
| b |
解答:解:∵向量
=(x1,y1),
=(x2,y2),
∴
-
=(x1-x2,y1-y2)
∵|
-
|=R,且
-
与
夹角为
,
=(1,0),
∴(
-
)•
=x1-x2=|
-
||
|cos
=
.
故选D.
| a |
| b |
∴
| a |
| b |
∵|
| a |
| b |
| a |
| b |
| e |
| π |
| 3 |
| e |
∴(
| a |
| b |
| e |
| a |
| b |
| e |
| π |
| 3 |
| R |
| 2 |
故选D.
点评:考查平面向量的坐标运算和数量积的定义,属基础题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
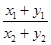 的值为( )
的值为( )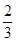 B.-
B.-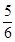 D.-
D.-