题目内容
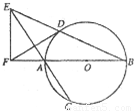
 如图AB是⊙O的直径,P为AB延长线上一点,PC切⊙O于点C,PC=4,PB=2则∠APC的正弦值等于
如图AB是⊙O的直径,P为AB延长线上一点,PC切⊙O于点C,PC=4,PB=2则∠APC的正弦值等于| 3 |
| 5 |
| 3 |
| 5 |
分析:连接OC,根据切割线定理得PC2=PA•PB,结合PC、PB长,算出PA=8,从而得到半径OC=OB=3,在Rt△OCP中,利用三角函数的定义,即可得到∠APC的正弦值.
解答: 解:连接OC,
解:连接OC,
∵PC切⊙O于点C,
∴OC⊥PC且PC2=PA•PB
∵PC=4,PB=2,
∴PA=
=8,可得直径AB=6,
∴OC=OB=3,OP=2+3=5
Rt△OCP中,sin∠APC=
=
故答案为:
 解:连接OC,
解:连接OC,∵PC切⊙O于点C,
∴OC⊥PC且PC2=PA•PB
∵PC=4,PB=2,
∴PA=
| PA 2 |
| PB |
∴OC=OB=3,OP=2+3=5
Rt△OCP中,sin∠APC=
| OC |
| OP |
| 3 |
| 5 |
故答案为:
| 3 |
| 5 |
点评:本题在圆的切线、割线的图形下,求一个角的正弦值,着重考查了切割线定理、切线的性质定理和直角三角形的三角函数定义等知识,属于基础题.

练习册系列答案
相关题目
 注意:在以下(1)(2)两题中任选一题.如果两题都做,按(1)给分.
注意:在以下(1)(2)两题中任选一题.如果两题都做,按(1)给分. (2012•郑州二模)选修4-1:平面几何
(2012•郑州二模)选修4-1:平面几何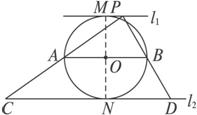
 ,EA=2AC,求AF的长.
,EA=2AC,求AF的长.