题目内容
已知动圆过定点A(0,2),且在x轴上截得的弦长为4.
(1)求动圆圆心的轨迹C的方程;
(2)点P为轨迹C上任意一点,直线l为轨迹C上在点P处的切线,直线l交直线:y=-1于点R,过点P作PQ⊥l交轨迹C于点Q,求△PQR的面积的最小值.
解 (1)设C(x,y),|CA|2-y2=4,即x2=4y.
∴动圆圆心的轨迹C的方程为x2=4y.
(2)C的方程为x2=4y,即y= x2,故y′=
x2,故y′= x.
x.


 则当t=2时,f(t)min=4.
则当t=2时,f(t)min=4.
由S△PQR= [f(t)]3,得△PQR的面积的最小值为16.
[f(t)]3,得△PQR的面积的最小值为16.

练习册系列答案
相关题目
已知x与y之间的几组数据如下表:
| x | 1 | 2 | 3 | 4 | 5 | 6 |
| y | 0 | 2 | 1 | 3 | 3 | 4 |
假设根据上表数据所得线性回归直线方程为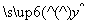 =
=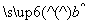 x+
x+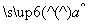 .若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( )
.若某同学根据上表中的前两组数据(1,0)和(2,2)求得的直线方程为y=b′x+a′,则以下结论正确的是( )
A.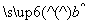 >b′,
>b′,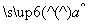 >a′ B.
>a′ B.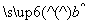 >b′,
>b′,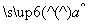 <a′
<a′
C.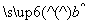 <b′,
<b′,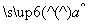 >a′ D.
>a′ D.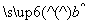 <b′,
<b′,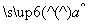 <a′
<a′
 的值为( )
的值为( ) =1的渐近线的距离是( )
=1的渐近线的距离是( ) B.
B.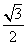

 -
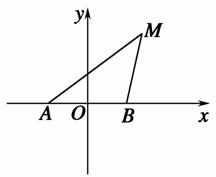
-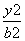 =1(a>0,b>0)与直线y=
=1(a>0,b>0)与直线y=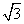 x无交点,则离心率e的取值范围是( )
x无交点,则离心率e的取值范围是( )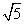 ) D.(1,
) D.(1,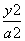 +
+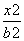 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为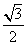 ,椭圆C的短轴的一个端点P到焦点的距离为2.
,椭圆C的短轴的一个端点P到焦点的距离为2.