题目内容
设平面 与平面
与平面 相交于直线
相交于直线 ,直线
,直线 在平面
在平面 内,直线
内,直线 在平面
在平面 内,且
内,且 ,则“
,则“ ”是“
”是“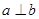 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |

解析试题分析:若 ,又
,又 ,根据两个平面垂直的性质定理可得
,根据两个平面垂直的性质定理可得 ,又因为
,又因为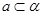 ,所以
,所以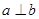 ;反过来,当
;反过来,当 时,因为
时,因为 ,一定有
,一定有 ,但不能保证
,但不能保证 ,即不能推出
,即不能推出 .
.
考点:充要条件的判断,线面垂直的性质.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知命题 ,命题
,命题 ,则( )
,则( )
A.命题 是假命题 是假命题 |
B.命题 是真命题 是真命题 |
C.命题 是真命题 是真命题 |
D.命题 是假命题 是假命题 |
若命题“ ”为假,且“
”为假,且“ ”为假,则( )
”为假,则( )
A.“ ”为假 ”为假 | B. 假 假 |
C. 真 真 | D.不能判断 的真假 的真假 |
设 为实数,则“
为实数,则“ 是
是 ”的( )
”的( )
| A.充分不必要 | B.必要不充分 |
| C.充要条件 | D.既不充分又不必要 |
已知函数 的定义域为
的定义域为 ,则
,则 的定义域为( )
的定义域为( )
A. | B. | C. | D. |
设偶函数 对任意
对任意 都有
都有 ,且当
,且当 时,
时, ,则
,则 ( )
( )
| A.10 | B. | C.-10 | D. |
 ,
, 则
则 =
=  ”的否命题为“若
”的否命题为“若 ”;
”; 则
则 ”的逆命题为真命题;
”的逆命题为真命题; ”的否定是“
”的否定是“ ”;
”;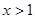 ”是“
”是“ ”的充分不必要条件.
”的充分不必要条件. ”的否定是__ __
”的否定是__ __