题目内容
命题“对任意 ”的否定是__ __
”的否定是__ __
存在 使得
使得 .
.
解析试题分析:命题“对任意 ”是全称命题,所以其否定是特称命题,故答案为存在
”是全称命题,所以其否定是特称命题,故答案为存在 使得
使得 .
.
考点: 命题的否定.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
如果命题 为真命题,
为真命题, 为假命题,那么( )
为假命题,那么( )
| A.命题p、q都是真命题 |
| B.命题p、q都是假命题 |
| C.命题p、q至少有一个是真命题 |
| D.命题p、q只有一个真命题 |
设 为实数,命题甲:
为实数,命题甲: ,命题乙:
,命题乙: ,则甲是乙的( )
,则甲是乙的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
设平面 与平面
与平面 相交于直线
相交于直线 ,直线
,直线 在平面
在平面 内,直线
内,直线 在平面
在平面 内,且
内,且 ,则“
,则“ ”是“
”是“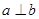 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
设 是定义在实数集
是定义在实数集 上的函数,且满足下列关系
上的函数,且满足下列关系 ,
, ,则
,则 是( ).
是( ).
| A.偶函数,但不是周期函数 | B.偶函数,又是周期函数 |
| C.奇函数,但不是周期函数 | D.奇函数,又是周期函数 |
下列四组函数,表示同一函数的是( ).
A. , , |
B. , , |
C. , , |
D. , ,  |
下列说法中,正确的是( )
A.对任意 ,都有 ,都有 ; ; |
B. 是 是 上的增函数; 上的增函数; |
C.若 且 且 ,则 ,则 ; ; |
| D.函数y=x|x|是R上的增函数 |
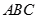 中,若
中,若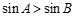 ,则
,则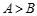 ”的否命题是真命题;
”的否命题是真命题;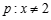 或
或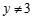 ,命题
,命题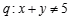 则
则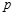 是
是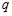 的必要不充分条件;
的必要不充分条件;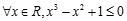 ”的否定是“
”的否定是“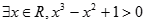 ”.
”. 的图象大致是( )
的图象大致是( )