题目内容
在数列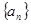 中,
中,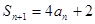 ,
,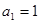 .
.
(1)设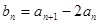 ,求证数列
,求证数列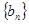 是等比数列;
是等比数列;
(2)求数列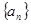 的通项公式.
的通项公式.
(1)

 所以数列
所以数列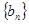 是等比数列
是等比数列
(2)
解析试题分析:(1) ,
,
 ,所以数列
,所以数列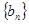 是等比数列
是等比数列
(2)由(1)知
 是等差数列,公差为
是等差数列,公差为 ,首项为
,首项为 ,所以通项为
,所以通项为
考点:等比数列的证明及数列求通项
点评:要证明一个数列是等比数列要依据定义,即证明数列的相邻两项的比值是固定的常数;在求一般数列的通项公式时,通常需要构造与之相关的数列为等差数列或等比数列,借助于这两个特殊数列求解

练习册系列答案
相关题目
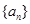 的前
的前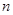 项和为
项和为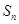 ,
,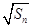 是
是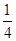 与
与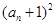 的等比中项.
的等比中项.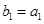 ,且
,且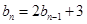 ,求数列
,求数列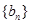 的通项公式;
的通项公式;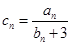 ,求数列
,求数列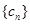 的前
的前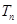 .
.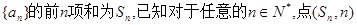 都在函数
都在函数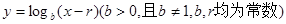 的图象上。
的图象上。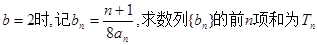 ;
;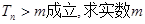 的取值范围。
的取值范围。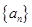 的首项
的首项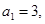 前
前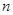 项和为
项和为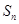 ,且
,且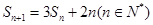 ,
,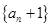 是否成等比数列?并求出数列
是否成等比数列?并求出数列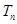 为数列
为数列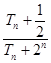 的最小值.
的最小值.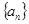 满足:
满足: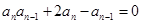 ,
, 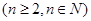 ,
, ,前
,前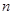 项和为
项和为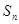 的数列
的数列 满足:
满足: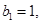
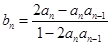
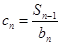
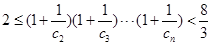
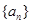 的前
的前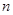 项和为
项和为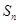 ,且
,且 ,
,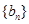 满足
满足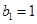 ,且点
,且点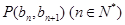 在直线
在直线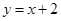 上.
上.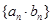 的前
的前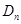 ;
;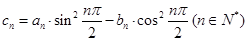 ,求数列
,求数列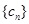 的前
的前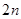 项和
项和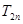 .
.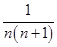 .
.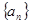 的通项公式为
的通项公式为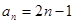 ,数列
,数列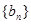 的前n项和为
的前n项和为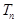 ,且满足
,且满足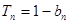
 中是否存在使得
中是否存在使得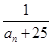 是
是 的前
的前 项和为
项和为 ,且
,且
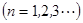 ,等差数列
,等差数列 中,
中, ,
,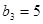 。
。 的通项
的通项 和
和 ;
; ,求数列
,求数列 的前
的前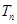 ,
,