在(1+x)n二项展开式中x2的系数为15.则${∫} {0}^{1}$xndx=( )A．$\frac{1}{7}$B．7C．15D．$\frac{10}{3}$ 题目和参考答案——青夏教育精英家教网—

题目内容

17．在（1+x）ⁿ（n∈N*）二项展开式中x²的系数为15，则${∫}_{0}^{1}$xⁿdx=（　　）

A．

$\frac{1}{7}$

B．

C．

D．

$\frac{10}{3}$

分析根据二项展开式的通项公式求出展开式的特定项，可得n，利用定积分即可得出结论．

解答解：由题意，${C}_{n}^{2}$=15，∴n=6，
∴${∫}_{0}^{1}$x⁶dx=$\frac{1}{7}{x}^{7}{|}_{0}^{1}$=$\frac{1}{7}$，
故选A．

点评本题考查了二项展开式通项公式的应用问题，考查定积分知识的运用，是基础题目．

练习册系列答案

8．已知函数f（x）=mlnx+（m-1）x（m∈R）．
（Ⅰ）当m=3时，求曲线y=f（x）在点（1，f（1））处的切线方程；
（Ⅱ）若f（x）存在最大值M，且M＞0，求m的取值范围．

5．已知k∈R，点P（a，b）是直线x+y=2k与圆x²+y²=k²-2k+3的公共点，则ab的最大值为（　　）

12．若角α的终边经过点P₀（-3，-4），则tanα=（　　）

2．已知f（x）是定义在（0，+∞）上的单调函数，且?x∈（0，+∞），f[f（x）-lnx]=e+1，设a=f（（$\frac{1}{2}$）${\;}^{\frac{1}{3}}$），b=f（（$\frac{1}{3}$）${\;}^{\frac{1}{2}}$），c=f（log₂π），则a，b，c的大小关系是c＞a＞b（用“＞”号连接表示）

9．已知f（x）=bx-b，g（x）=（bx-1）e^x，b∈R
（Ⅰ）若b≥0，讨论g（x）的单调性；
（Ⅱ）若不等式f（x）＞g（x）有且仅有两个整数解，求b的取值范围．

6．

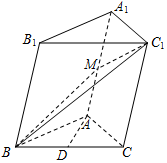在斜三棱柱ABC-A₁B₁C₁中，AB=AC，平面BB₁C₁C⊥底面ABC，点M、D分别是线段AA₁、BC的中点．
（1）求证：AD⊥CC₁；
（2）求证：AD∥平面MBC₁．

7．设点F为抛物线y²=4x的焦点，A，B是抛物线上两点，线段AB的中垂线交x轴于点D（5，0），则|AF|+|BF|=（　　）

试题分类