题目内容
设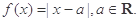
(1)当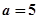 ,解不等式
,解不等式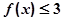 ;
;
(2)当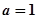 时,若
时,若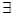
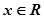 ,使得不等式
,使得不等式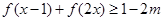 成立,求实数
成立,求实数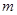 的取值范围.
的取值范围.
(I) ;(II)
;(II) .
.
解析试题分析:(I)绝对值不等式的解法,易知不等式的等价不等式组解出不等式解集; (II)存在性问题转化为函数最值问题,含绝对值的函数式去绝对值化为分段函数求得最值即可.
试题解析:(I) 时原不等式等价于
时原不等式等价于 即
即 ,所以解集为
,所以解集为 .
.
(II)当 时,
时, ,令
,令 ,
,
由图像知:当 时,
时, 取得最小值
取得最小值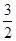 ,由题意知:
,由题意知: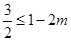 ,所以实数
,所以实数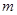 的取值范围为
的取值范围为 .
.
考点:1、绝对值不等式的解法; 2、函数最值问题.

练习册系列答案
相关题目
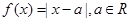
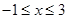 时,
时,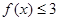 ,求a的取值范围;
,求a的取值范围;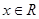 ,
,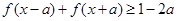 恒成立,求实数a的最小值
恒成立,求实数a的最小值 是定义在
是定义在 上的偶函数,
上的偶函数, ,当
,当 时,
时, .
. ;
;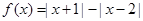 .
.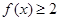 ;
;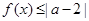 的解集为
的解集为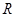 ,求实数
,求实数 的取值范围.
的取值范围.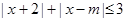 的解集为
的解集为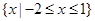 .
. 的值;
的值;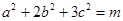 ,求
,求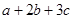 的取值范围.
的取值范围.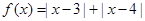 .
. ;
; ,
,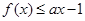 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.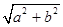 ≥
≥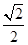 (a+b).
(a+b). 的不等式
的不等式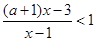 .
. 时,解该不等式;
时,解该不等式; 时,解该不等式.
时,解该不等式.