题目内容
19、如图,点A、B分别是椭圆(1)求点P的坐标;
(2)设M是椭圆长轴AB上的一点,M到直线AP的距离等于![]() ,求椭圆上的点到点M的距离
,求椭圆上的点到点M的距离![]() 的最小值。
的最小值。
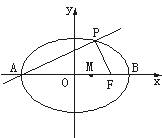
19.[解](1)由已知可得点A(-6,0),F(4,0),
设点P的坐标是(x,y),则![]() ={x+6,y},
={x+6,y}, ![]() ={x-4,y},由已知得
={x-4,y},由已知得
![]()
![]() (x+6)(x-4)+y2=0
(x+6)(x-4)+y2=0
则2x2+9x-18=0. x=![]() 或x=-6.
或x=-6.
由于y>0,只能x=![]() .于是y=
.于是y=![]() .
.
∴点P的坐标是(![]() ,
,![]() ).
).
(2)直线AP的方程是x-![]() y+6=0.
y+6=0.
设点M的坐标是(m,0),则M到直线AP的距离是![]() ,
,
于是![]() =|m-6|, 又-6≤m≤6,解得m=2,
=|m-6|, 又-6≤m≤6,解得m=2,
椭圆上的点(x,y)到点M的距离d有
d2=(x-2)2+y2
=x2-4x+4+20-![]() x2
x2
=![]()
由于-6≤x≤6,
∴x=![]() 时,d取得最小值
时,d取得最小值![]() 。
。

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
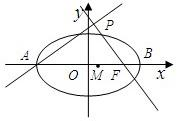 如图,点A,B分别是椭圆
如图,点A,B分别是椭圆 如图,点A、B分别是椭圆长轴的左、右端点,点F是椭圆的右焦点,其中A(-6,0),F(4,0),点P在椭圆上且位于x轴上方,
如图,点A、B分别是椭圆长轴的左、右端点,点F是椭圆的右焦点,其中A(-6,0),F(4,0),点P在椭圆上且位于x轴上方, 如图,点A、B分别是椭圆
如图,点A、B分别是椭圆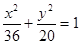 长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于
长轴的左、右端点,点F是椭圆的右焦点,点P在椭圆上,且位于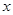 轴上方,
轴上方,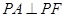 .
.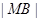 ,求椭圆上的点到点M的距离
,求椭圆上的点到点M的距离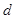 的最小值.
的最小值.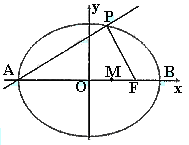
 的长轴的左右端点,点F为椭圆的右焦点,直线PF的方程为:
的长轴的左右端点,点F为椭圆的右焦点,直线PF的方程为: 且
且 。
。
 ,求椭圆上的点到
,求椭圆上的点到