题目内容
设双曲线 -
- =1(0<a<b)的半焦距为c,直线L过(a,0),(0,b),且原点到L的距离为
=1(0<a<b)的半焦距为c,直线L过(a,0),(0,b),且原点到L的距离为 c,则双曲线的离心率为
c,则双曲线的离心率为
- A.

- B.

- C.

- D.
 或
或
A
分析:直线L的方程为 ,即bx+ay-ab=0,由点到直线的距离公式,得
,即bx+ay-ab=0,由点到直线的距离公式,得 ,3ab=
,3ab= ,由此能求出双曲线的离心率.
,由此能求出双曲线的离心率.
解答:直线L的方程为 ,即bx+ay-ab=0,
,即bx+ay-ab=0,
由点到直线的距离公式,得 ,
,
∴3ab= ,
,
∴9a2(c2-a2)=2c4,
∴2e4-9e2+9=0,
解得 或
或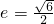 .
.
∵0<a<b,∴e= .
.
故选A.
点评:本题考查双曲线的性质和应用,解题时要认真审题,仔细解答.
分析:直线L的方程为
 ,即bx+ay-ab=0,由点到直线的距离公式,得
,即bx+ay-ab=0,由点到直线的距离公式,得 ,3ab=
,3ab= ,由此能求出双曲线的离心率.
,由此能求出双曲线的离心率.解答:直线L的方程为
 ,即bx+ay-ab=0,
,即bx+ay-ab=0,由点到直线的距离公式,得
 ,
,∴3ab=
 ,
,∴9a2(c2-a2)=2c4,
∴2e4-9e2+9=0,
解得
 或
或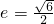 .
.∵0<a<b,∴e=
 .
.故选A.
点评:本题考查双曲线的性质和应用,解题时要认真审题,仔细解答.

练习册系列答案
相关题目
 =1(0<a<b=的半焦距为c,直线l过(a,0),(0,b)两点.已知原点到直线l的距离为
=1(0<a<b=的半焦距为c,直线l过(a,0),(0,b)两点.已知原点到直线l的距离为 c,则双曲线的离心率为 ( )
c,则双曲线的离心率为 ( ) C.
C. D.
D.
 =1(0<a<b)的半焦距为c,直线l过(a,0)(0,b)两点,已知原点到直线l的距离为
=1(0<a<b)的半焦距为c,直线l过(a,0)(0,b)两点,已知原点到直线l的距离为 ,则双曲线的离心率为( )
,则双曲线的离心率为( )


 =1(0<a<b)的半焦距为c,直线l过(a,0)(0,b)两点,已知原点到直线l的距离为
=1(0<a<b)的半焦距为c,直线l过(a,0)(0,b)两点,已知原点到直线l的距离为 ,则双曲线的离心率为( )
,则双曲线的离心率为( )


 =1(0<a<b)的半焦距为c,直线l过(a,0)(0,b)两点,已知原点到直线l的距离为
=1(0<a<b)的半焦距为c,直线l过(a,0)(0,b)两点,已知原点到直线l的距离为 ,则双曲线的离心率为( )
,则双曲线的离心率为( )


 =1(0<a<b)的半焦距为c,直线l过(a,0)(0,b)两点,已知原点到直线l的距离为
=1(0<a<b)的半焦距为c,直线l过(a,0)(0,b)两点,已知原点到直线l的距离为 ,则双曲线的离心率为( )
,则双曲线的离心率为( )

