题目内容
设二次函数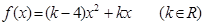 ,对任意实数
,对任意实数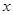 ,
,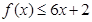 恒成立;正数数列
恒成立;正数数列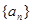 满足
满足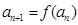 .
.
(1)求函数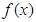 的解析式和值域;
的解析式和值域;
(2)试写出一个区间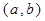 ,使得当
,使得当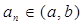 时,数列
时,数列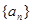 在这个区间上是递增数列,并说明理由;
在这个区间上是递增数列,并说明理由;
(3)若已知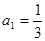 ,求证:数列
,求证:数列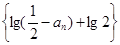 是等比数列
是等比数列
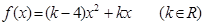 ,对任意实数
,对任意实数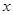 ,
,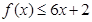 恒成立;正数数列
恒成立;正数数列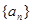 满足
满足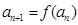 .
.(1)求函数
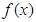 的解析式和值域;
的解析式和值域;(2)试写出一个区间
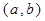 ,使得当
,使得当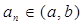 时,数列
时,数列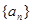 在这个区间上是递增数列,并说明理由;
在这个区间上是递增数列,并说明理由;(3)若已知
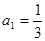 ,求证:数列
,求证:数列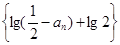 是等比数列
是等比数列解:(1)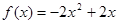 其值域为
其值域为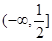 .…………4分
.…………4分
(2)解:当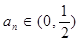 时,数列
时,数列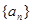 在这个区间上是递增数列,证明如下:
在这个区间上是递增数列,证明如下:
设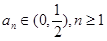 ,则
,则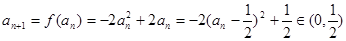 ,所以对一切
,所以对一切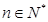 ,均有
,均有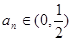 ;………6分
;………6分
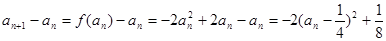
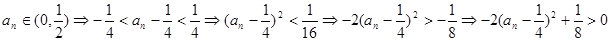 ,
,
从而得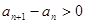 ,即
,即 ,所以数列
,所以数列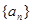 在区间
在区间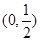 上是递增数列.………8分
上是递增数列.………8分
注:本题的区间也可以是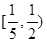 、
、 、
、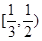 等无穷多个.
等无穷多个.
另解:若数列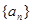 在某个区间上是递增数列,则
在某个区间上是递增数列,则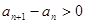
即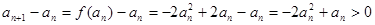
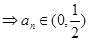 ……6分
……6分
又当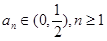 时,
时,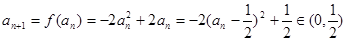 ,所以对一切
,所以对一切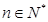 ,均有
,均有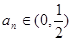 且
且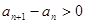 ,所以数列
,所以数列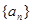 在区间
在区间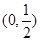 上是递增数列.
上是递增数列.
(3)证明略
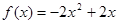 其值域为
其值域为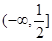 .…………4分
.…………4分(2)解:当
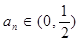 时,数列
时,数列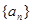 在这个区间上是递增数列,证明如下:
在这个区间上是递增数列,证明如下:设
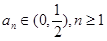 ,则
,则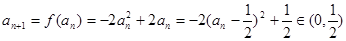 ,所以对一切
,所以对一切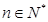 ,均有
,均有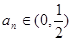 ;………6分
;………6分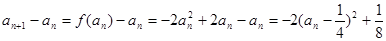
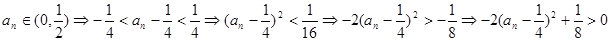 ,
,从而得
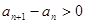 ,即
,即 ,所以数列
,所以数列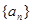 在区间
在区间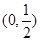 上是递增数列.………8分
上是递增数列.………8分注:本题的区间也可以是
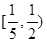 、
、 、
、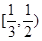 等无穷多个.
等无穷多个.另解:若数列
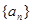 在某个区间上是递增数列,则
在某个区间上是递增数列,则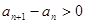
即
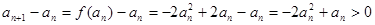
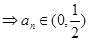 ……6分
……6分又当
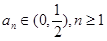 时,
时,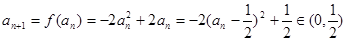 ,所以对一切
,所以对一切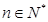 ,均有
,均有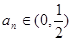 且
且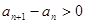 ,所以数列
,所以数列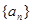 在区间
在区间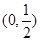 上是递增数列.
上是递增数列.(3)证明略
本试题主要是考查了函数的解析式和值域以及函数单调性的运用,以及等比数列的定义的综合问题。
(1)由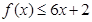 恒成立等价于
恒成立等价于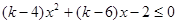 恒成立转化为判别式的不等式得到参数k的值,进而求解。
恒成立转化为判别式的不等式得到参数k的值,进而求解。
(2)利用数列的单调性的定义,若数列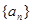 在某个区间上是递增数列,则
在某个区间上是递增数列,则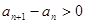
即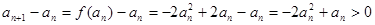
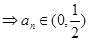
(3)由(2)知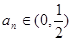 ,从而
,从而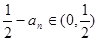 ,即
,即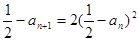 得到数列
得到数列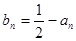 的递推关系,进而求解得到。
的递推关系,进而求解得到。
(1)由
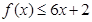 恒成立等价于
恒成立等价于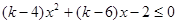 恒成立转化为判别式的不等式得到参数k的值,进而求解。
恒成立转化为判别式的不等式得到参数k的值,进而求解。(2)利用数列的单调性的定义,若数列
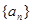 在某个区间上是递增数列,则
在某个区间上是递增数列,则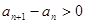
即
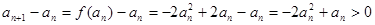
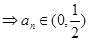
(3)由(2)知
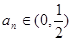 ,从而
,从而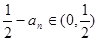 ,即
,即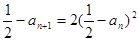 得到数列
得到数列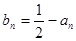 的递推关系,进而求解得到。
的递推关系,进而求解得到。
练习册系列答案
相关题目
 的前
的前 项和为
项和为 ,
, (
(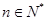 ).
). 是等比数列,求出数列
是等比数列,求出数列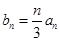 ,求数列
,求数列 的前
的前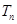 ;
;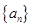 中,
中,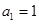 ,
, .
.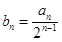 .证明:数列
.证明:数列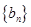 是等差数列;
是等差数列;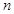 项和
项和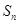 .
.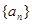 、
、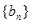 都是公差为1的等差数列,其首项分别为
都是公差为1的等差数列,其首项分别为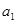 、
、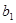 ,且
,且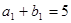 ,
, 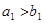 ,
,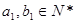 ,
,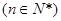 ,则数列
,则数列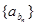 前10项的和等于( )
前10项的和等于( )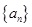 的前5项的和为30,前10项的和为100,则它的前15的和为( )
的前5项的和为30,前10项的和为100,则它的前15的和为( )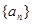 为等差数列,若
为等差数列,若 ,且它的前
,且它的前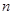 项和
项和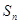 有最小值,那么当
有最小值,那么当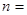
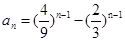 ,则数列{an}
,则数列{an} 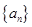 的前n项和为
的前n项和为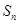 ,若
,若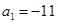 ,
,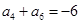 ,则当
,则当