题目内容
(本小题满分12分)已知椭圆的中心在原点,焦点在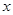 轴上,离心率为
轴上,离心率为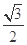 ,且经过点
,且经过点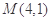 ,直线
,直线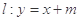 交椭圆于不同的两点
交椭圆于不同的两点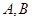 .
.
(1)求椭圆的方程;
(2)求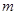 的取值范围;
的取值范围;
(3)若直线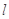 不过点
不过点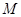 ,求证:直线
,求证:直线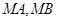 与
与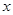 轴围成一个等腰三角形.
轴围成一个等腰三角形.
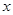 轴上,离心率为
轴上,离心率为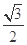 ,且经过点
,且经过点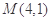 ,直线
,直线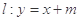 交椭圆于不同的两点
交椭圆于不同的两点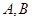 .
.(1)求椭圆的方程;
(2)求
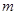 的取值范围;
的取值范围;(3)若直线
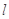 不过点
不过点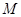 ,求证:直线
,求证:直线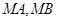 与
与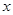 轴围成一个等腰三角形.
轴围成一个等腰三角形.(1)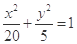 (2)
(2)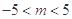 (3)见解析
(3)见解析
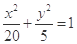 (2)
(2)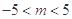 (3)见解析
(3)见解析试题分析:(1)由已知椭圆焦点在
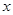 轴上可设椭圆的方程为
轴上可设椭圆的方程为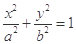 ,(
,(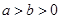 )
)因为
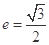 ,所以
,所以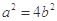 , ①
, ①又因为过点
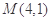 ,所以
,所以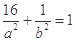 , ②
, ②联立①②解得
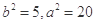 ,故椭圆方程为
,故椭圆方程为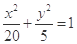 . ……4分
. ……4分(2)将
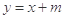 代入
代入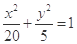 并整理得
并整理得 ,
,因为直线与椭圆有两个交点,
所以
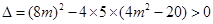 ,解得
,解得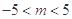 . ……8分
. ……8分(3)设直线
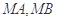 的斜率分别为
的斜率分别为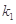 和
和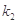 ,只要证明
,只要证明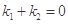 即可.
即可.设
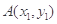 ,
,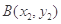 ,
,则
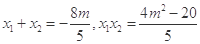 .
.所以
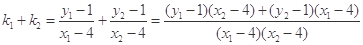
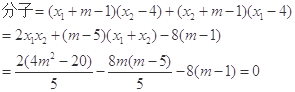
所以
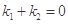 ,所以直线
,所以直线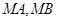 与
与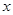 轴围成一个等腰三角形. ……12分
轴围成一个等腰三角形. ……12分点评:纵观历年高考,椭圆是一个高频考点,题型有选择题和填空题,难度不大,但解答题是压轴题,难度较大,所以在学习中,同学们一方面要掌握好椭圆的标准方程和几何性质等基础知识,另外还要多归纳这些知识的使用方法和应用技巧,做到心中有数,从容应对.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
 , 则以M(4,1)为中点的弦所在直线l的方程是 .
, 则以M(4,1)为中点的弦所在直线l的方程是 . 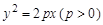 的焦点与椭圆
的焦点与椭圆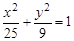 的一个焦点重合,过点
的一个焦点重合,过点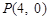 的直线与抛物线交于
的直线与抛物线交于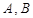 两点,若
两点,若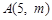 ,则
,则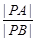 的值( )
的值( )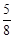
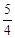
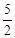
 和F分别为椭圆
和F分别为椭圆
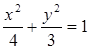 的中心和左焦点,点P为椭圆上的任意点,则
的中心和左焦点,点P为椭圆上的任意点,则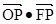 的最大值是( )
的最大值是( ) 和点
和点 ,.斜率为
,.斜率为 的直线与抛物线
的直线与抛物线 相交不同的两个点
相交不同的两个点 .若点
.若点 恰好为
恰好为 的中点.
的中点. ,使得经过点
,使得经过点 的圆和抛物线
的圆和抛物线 的左焦点为
的左焦点为 ,
, 是两个顶点,如果
是两个顶点,如果 的距离等于
的距离等于 ,则椭圆的离心率为 .
,则椭圆的离心率为 .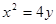 的焦点F作直线交抛物线于
的焦点F作直线交抛物线于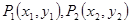 两点,若
两点,若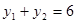 ,则
,则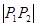 的值为( )
的值为( )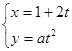 ,(t为参数,a∈R)点M(5,4)在该曲线上,(1)求常数a;(2)求曲线C的普通方程。
,(t为参数,a∈R)点M(5,4)在该曲线上,(1)求常数a;(2)求曲线C的普通方程。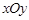 中,若双曲线
中,若双曲线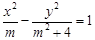 的离心率为
的离心率为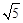 ,则
,则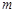 的值为 .
的值为 .