题目内容
已知抛物线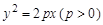 的焦点与椭圆
的焦点与椭圆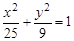 的一个焦点重合,过点
的一个焦点重合,过点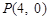 的直线与抛物线交于
的直线与抛物线交于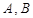 两点,若
两点,若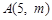 ,则
,则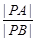 的值( )
的值( )
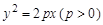 的焦点与椭圆
的焦点与椭圆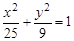 的一个焦点重合,过点
的一个焦点重合,过点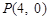 的直线与抛物线交于
的直线与抛物线交于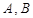 两点,若
两点,若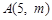 ,则
,则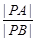 的值( )
的值( )A.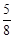 | B.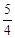 | C.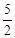 | D.3 |
B
试题分析:易知抛物线方程为
 ,所以A点坐标为
,所以A点坐标为 ,又点A、P求出直线AB的方程为:
,又点A、P求出直线AB的方程为: ,联立方程组:
,联立方程组: 解得B的横坐标为
解得B的横坐标为 ,由抛物线的定义知
,由抛物线的定义知 ,
, ,所以
,所以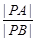 的值为
的值为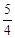 。
。点评:本题考查直线和抛物线的性质的灵活应用,属于中档题。解题时要认真审题,仔细计算,注意合理地进行等价转化.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
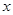 轴上,离心率为
轴上,离心率为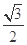 ,且经过点
,且经过点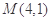 ,直线
,直线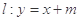 交椭圆于不同的两点
交椭圆于不同的两点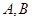 .
.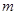 的取值范围;
的取值范围;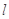 不过点
不过点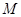 ,求证:直线
,求证:直线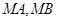 与
与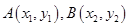 ,定义它们之间的一种“距离”:
,定义它们之间的一种“距离”: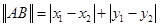 .给出下列三个命题:
.给出下列三个命题: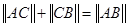 ;
;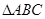 中,若∠C=90°,则
中,若∠C=90°,则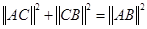 ;
;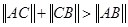 .
.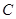 :
: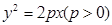 过点
过点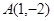 .(1)求抛物线
.(1)求抛物线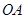 (
(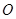 为坐标原点)的直线
为坐标原点)的直线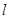 ,使得直线
,使得直线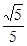 ?若存在,求出直线
?若存在,求出直线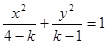 表示的曲线为
表示的曲线为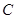 ,给出下列四个命题:
,给出下列四个命题: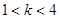 ,则曲线
,则曲线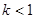 或
或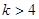 ;④若曲线
;④若曲线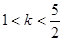 .
. ,则离心率为 .
,则离心率为 . 的中心,而焦点是双曲线的顶点,求抛物线的方程.
的中心,而焦点是双曲线的顶点,求抛物线的方程.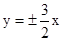 ,则其离心率是为 .
,则其离心率是为 .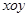 上取两个定点
上取两个定点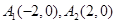 ,再取两个动点
,再取两个动点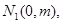
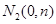 ,且
,且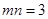 .
.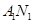 与
与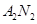 交点的轨迹
交点的轨迹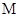 的方程;
的方程;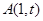 (
(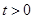 )是轨迹
)是轨迹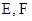 是轨迹
是轨迹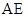 的斜率
的斜率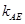 与直线
与直线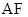 的斜率
的斜率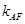 满足
满足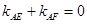 ,试探究直线
,试探究直线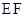 的斜率是否是定值?若是定值,求出这个定值,若不是,说明理由.
的斜率是否是定值?若是定值,求出这个定值,若不是,说明理由.