题目内容
17.点P在直线3x+4y-10=0上,过点P作圆x2+y2=1的切线,切点为M,则$\overrightarrow{PM}$•$\overrightarrow{PO}$(O是坐标原点)的最小值是( )| A. | 2 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 3 |
分析 作出图形,可得到$\overrightarrow{PM}•\overrightarrow{PO}=|\overrightarrow{PM}{|}^{2}=P{O}^{2}-1$,从而问题转化为求PO的最小值,而O到直线3x+4y-10=0的距离便是PO的最小值,根据点到直线的距离公式便可求出PO的最小值,从而得出$\overrightarrow{PM}•\overrightarrow{PO}$的最小值.
解答 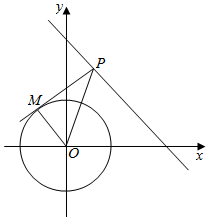 解:如图,
解:如图,
$\overrightarrow{PM}•\overrightarrow{PO}=|\overrightarrow{PM}||\overrightarrow{PO}|cos∠MPO$=$|\overrightarrow{PM}{|}^{2}$=PO2-1;
PO的最小值为O到直线3x+4y-10=0的距离:$\frac{10}{5}=2$;
∴$\overrightarrow{PM}•\overrightarrow{PO}$的最小值为3.
故选:D.
点评 考查向量数量积的计算公式,圆心和切点的连线与切线垂直,余弦函数的定义,直角三角形边的关系,以及点到直线的距离公式.

练习册系列答案
 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案
相关题目
7.已知变量x与y线性相关,且由观测数据算得样本平均数分别为$\overline{x}$=4,$\overline{y}$=3,则由该观测数据算得的线性回归方程不可能是( )
| A. | $\widehat{y}$=0.2x+2.2 | B. | $\widehat{y}$=0.3x+1.8 | C. | $\widehat{y}$=0.4x+1.4 | D. | $\widehat{y}$=0.5x+1.2 |
9.某校选定甲、乙、丙、丁、戊共5名教师到3个边远地区支教,每地至少1人,其中甲和乙一定不去同一地区,甲和丙必须去同一地区,则不同的选派方案共有( )
| A. | 27种 | B. | 30种 | C. | 33种 | D. | 36种 |

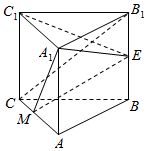 如图.在三棱柱ABC-A1B1C1中,已知侧棱与底面垂直,∠CAB=90°,且AC=1,AB=2,E为BB1的中点,M为AC上一点,$\overrightarrow{AM}$=$\frac{2}{3}$$\overrightarrow{AC}$.
如图.在三棱柱ABC-A1B1C1中,已知侧棱与底面垂直,∠CAB=90°,且AC=1,AB=2,E为BB1的中点,M为AC上一点,$\overrightarrow{AM}$=$\frac{2}{3}$$\overrightarrow{AC}$.