题目内容
6、设a,b,c,d∈(0,+∞),若a+d=b+c且|a-d|<|b-c|,则有( )
分析:|a-d|<|b-c|?(a-d)2<(b-c)2,化简后再利用(a+d)2=(b+c)2可得结论.
解答:解:|a-d|<|b-c|?(a-d)2<(b-c)2 ?a2+d2-2ad<b2+c2-2bc,
又∵a+d=b+c?(a+d)2=(b+c)2?a2+d2+2ad=b2+c2+2bc,
∴-4ad<-4bc,∴ad>bc.
故选C.
又∵a+d=b+c?(a+d)2=(b+c)2?a2+d2+2ad=b2+c2+2bc,
∴-4ad<-4bc,∴ad>bc.
故选C.
点评:本题考查不等式的性质,相等的两个实数的平方相等,两个不相等非负实数,分别平方后,原来大的仍然大.

练习册系列答案
相关题目
设A,B,C,D四点的坐标依次为(-1,0),(0,2),(4,3),(3,1),则四边形ABCD是( )
| A、正方形 | B、矩形 | C、菱形 | D、平行四边形 |
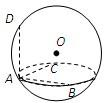 如图,设A、B、C、D为球O上四点,若AB、AC、AD两两互相垂直,且
如图,设A、B、C、D为球O上四点,若AB、AC、AD两两互相垂直,且