题目内容
如图所示,我炮兵阵地位于地面A处,两观察所分别位于地面C处和D处,已知CD=6000 m,∠ACD=45°,∠ADC=75°,目标出现于地面B处时测得∠BCD=30°,∠BDC=15°,则炮兵阵地到目标的距离是 (结果保留根号).
【答案】分析:根据∠ACD和∠ADC利用三角形内角和求得∠CAD,进而根据正弦定理求得AD,进而在△BCD中,利用正弦定理求得BD,最后在
Rt△ABD中,利用勾股定理求得AB.
解答:解:∵∠ACD=45°,∠ADC=75°,
∴∠CAD=60°.
在△ACD中,由正弦定理可得
 =
= ,
,
∴AD=6000× =2000
=2000 .
.
在△BCD中,由正弦定理得 =
= ,
,
∴BD= =3000
=3000
在Rt△ABD中,由勾股定可得AB2=BD2+AD2,
∴|AB|= =1000
=1000 (m).
(m).
答案1000 m
m
点评:本题主要考查了解三角形的实际应用.考查了学生运用所学知识解决实际问题的能力.
Rt△ABD中,利用勾股定理求得AB.
解答:解:∵∠ACD=45°,∠ADC=75°,
∴∠CAD=60°.
在△ACD中,由正弦定理可得
 =
= ,
,∴AD=6000×
 =2000
=2000 .
.在△BCD中,由正弦定理得
 =
= ,
,∴BD=
 =3000
=3000
在Rt△ABD中,由勾股定可得AB2=BD2+AD2,
∴|AB|=
 =1000
=1000 (m).
(m).答案1000
 m
m点评:本题主要考查了解三角形的实际应用.考查了学生运用所学知识解决实际问题的能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
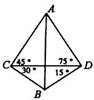 我炮兵阵地位于地面A处,两观察所分别位于地面点C和D处,已知DC=6000米,∠ACD=45°,∠ADC=75°,目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图所示).求炮兵阵地到目标的距离(结果保留根号).
我炮兵阵地位于地面A处,两观察所分别位于地面点C和D处,已知DC=6000米,∠ACD=45°,∠ADC=75°,目标出现于地面点B处时,测得∠BCD=30°,∠BDC=15°(如图所示).求炮兵阵地到目标的距离(结果保留根号). 如图所示,我炮兵阵地位于地面A处,两观察所分别位于地面C处和D处,已知CD=6000 m,∠ACD=45°,∠ADC=75°,目标出现于地面B处时测得∠BCD=30°,∠BDC=15°,则炮兵阵地到目标的距离是
如图所示,我炮兵阵地位于地面A处,两观察所分别位于地面C处和D处,已知CD=6000 m,∠ACD=45°,∠ADC=75°,目标出现于地面B处时测得∠BCD=30°,∠BDC=15°,则炮兵阵地到目标的距离是
