题目内容
已知:点A(2,2)、点B(4,4)、点C(4,2)是⊙D上的三个点.
(Ⅰ)求⊙D的一般方程;
(Ⅱ)直线l:x-y-4=0,点P在直线l上运动,过点P作⊙D的两贴切线,切点分别是M、N,求当PD⊥l时四边形PMDN的面积,并求这时点P的坐标.
(Ⅰ)求⊙D的一般方程;
(Ⅱ)直线l:x-y-4=0,点P在直线l上运动,过点P作⊙D的两贴切线,切点分别是M、N,求当PD⊥l时四边形PMDN的面积,并求这时点P的坐标.
考点:直线的一般式方程
专题:直线与圆
分析:(Ⅰ)设⊙D的一般方程为x2+y2+dx+ey+f=0,
由题意列式求出d,e,f,则⊙D的一般方程可求;
(Ⅱ)由(Ⅰ)知⊙D的圆心D(3,3),根据PD⊥l可得PD方程,联立两直线方程求得P(5,1),再由圆心D到直线l的距离结合直角三角形求得半径r,
根据对称性可得SPMDN=2S△PMD=2×
|PM|•|MD|=r
=
•
.则四边形PMDN的面积可求.
由题意列式求出d,e,f,则⊙D的一般方程可求;
(Ⅱ)由(Ⅰ)知⊙D的圆心D(3,3),根据PD⊥l可得PD方程,联立两直线方程求得P(5,1),再由圆心D到直线l的距离结合直角三角形求得半径r,
根据对称性可得SPMDN=2S△PMD=2×
| 1 |
| 2 |
| |PD|2-r2 |
| 2 |
| |PD|2-2 |
解答:
解:(Ⅰ)设⊙D的一般方程为x2+y2+dx+ey+f=0,
则
,解得
.
∴⊙D的一般方程为x2+y2-6x-6y+16=0;
(Ⅱ)由(Ⅰ)知⊙D的圆心D(3,3),
由PD⊥l,可设PD:x+y+m=0,解得:m=-6.
∴
,解得:P(5,1),
这时圆心D到直线l的距离|PD|=h=
=2
.
⊙D的半径r=
=
.
h>r,∴直线l与⊙D无公共点,
根据对称性,SPMDN=2S△PMD=2×
|PM|•|MD|
=r
=
•
.
故SPMDN=
•
=2
.
综上,当P(5,1)时,SPMDN=2
.
则
|
|
∴⊙D的一般方程为x2+y2-6x-6y+16=0;
(Ⅱ)由(Ⅰ)知⊙D的圆心D(3,3),
由PD⊥l,可设PD:x+y+m=0,解得:m=-6.
∴
|
这时圆心D到直线l的距离|PD|=h=
| |3-3-4| | ||
|
| 2 |
⊙D的半径r=
| ||
| 2 |
| 2 |
h>r,∴直线l与⊙D无公共点,
根据对称性,SPMDN=2S△PMD=2×
| 1 |
| 2 |
=r
| |PD|2-r2 |
| 2 |
| |PD|2-2 |
故SPMDN=
| 2 |
(2
|
| 3 |
综上,当P(5,1)时,SPMDN=2
| 3 |
点评:本题考查了直线的一般式方程,考查了直线和圆的位置关系,考查了数学转化思想方法,是中档题.

练习册系列答案
相关题目
已知a,b为正数,且满足2<a+2b<4,那么3a-b的取值范围是( )
| A、(-4,6) |
| B、(-2,6) |
| C、(-4,12) |
| D、(-2,12) |
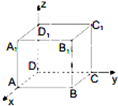 如图,把棱长为2的正方体ABCD-A1B1C1D1放在空间直角坐标系中,使D与原点重合,点A与点C分别放在x轴和y轴的正半轴上,则B1的坐标为:( )
如图,把棱长为2的正方体ABCD-A1B1C1D1放在空间直角坐标系中,使D与原点重合,点A与点C分别放在x轴和y轴的正半轴上,则B1的坐标为:( )| A、(2,2,2) |
| B、(2,2,0) |
| C、(2,0,2) |
| D、(0,2,2) |
下列函数中,在(0,+∞)上单调递增,并且是偶函数的是( )
| A、y=-x2 |
| B、y=-x3 |
| C、y=lg|x| |
| D、y=2x |
 如图所示曲线是幂函数y=xa在第一象限内的图象,其中a=±
如图所示曲线是幂函数y=xa在第一象限内的图象,其中a=±| 1 |
| 2 |
A、
| ||||
B、2、
| ||||
C、-
| ||||
D、2、
|
cos480°的值为( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|

 在△ABC中,角A、B、C所对的边分别是a、b、c,若∠C=
在△ABC中,角A、B、C所对的边分别是a、b、c,若∠C=