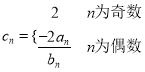题目内容
【题目】已知函数![]() 。
。
(Ⅰ)求函数![]() 的单调区间;
的单调区间;
(Ⅱ)若函数![]() 在
在![]() 上是减函数,求实数
上是减函数,求实数![]() 的取值范围。
的取值范围。
【答案】(1) 函数f(x)的单调递减区间是(0, ![]() );单调递增区间是(
);单调递增区间是(![]() ,+∞);(2) a≤-
,+∞);(2) a≤-![]() .
.
【解析】试题分析:(Ⅰ)先求出函数的导数,再通过讨论a的范围,从而求出其单调区间,(Ⅱ)由g(x)=![]() +x2+2aln x得g′(x)=-
+x2+2aln x得g′(x)=-![]() +2x+
+2x+![]() ,建立新函数,求出其最小值,解出即可.
,建立新函数,求出其最小值,解出即可.
试题解析:
(Ⅰ)函数f(x)的定义域为(0,+∞).
①当a≥0时,f′(x)>0,f(x)的单调递增区间为(0,+∞);
②当a<0时,f′(x)=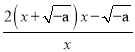 .
.
当x变化时,f′(x),f(x)的变化情况如下:
x | (0, |
| ( |
f′(x) | - | 0 | + |
f(x) |
| 极小值 |
|
由上表可知,函数f(x)的单调递减区间是(0, ![]() );单调递增区间是(
);单调递增区间是(![]() ,+∞).
,+∞).
(Ⅱ )由g(x)=![]() +x2+2aln x,得g′(x)=-
+x2+2aln x,得g′(x)=-![]() +2x+
+2x+![]() ,
,
由已知函数g(x)为[1,2]上的单调减函数,则g′(x)≤0在[1,2]上恒成立,
即-![]() +2x+
+2x+![]() ≤0在[1,2]上恒成立.即a≤
≤0在[1,2]上恒成立.即a≤![]() -x2在[1,2]上恒成立.
-x2在[1,2]上恒成立.
令![]() ,则h′(x)=-
,则h′(x)=-![]() -2x=-(
-2x=-(![]() +2x)
+2x)
![]()
![]() ,所以h(x)在[1,2]上为减函数,
,所以h(x)在[1,2]上为减函数,
h(x)min=h(2)=-![]() , 所以a≤-
, 所以a≤-![]() .
.

【题目】某校举行汉字听写比赛,为了了解本次比赛成绩情况,从得分不低于50分的试卷中随机抽取100名学生的成绩(得分均为整数,满分100分)进行统计,请根据频率分布表中所提供的数据,解答下列问题:
组号 | 分组 | 频数 | 频率 |
第1组 | [50,60) | 5 | 0.05 |
第2组 | [60,70) |
| 0.35 |
第3组 | [70,80) | 30 |
|
第4组 | [80,90) | 20 | 0.20 |
第5组 | [90,100] | 10 | 0.10 |
合计 | 100 | 1.00 |
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若从成绩较好的第3、4、5组中按分层抽样的方法抽取6人参加市汉字听写比赛,并从中选出2人做种子选手,求2人中至少有1人是第4组的概率。