题目内容
已知单调递增的等比数列 满足:
满足: ,且
,且
 是
是 的等差中项.
的等差中项.
(1)求数列 的通项公式;
的通项公式;
(2)若 ,
, ,求使
,求使 成立的正整数
成立的正整数 的最小值.
的最小值.
(1) (2)
(2)
【解析】
试题分析: 先设等比数列 的首项为
的首项为 ,公比为
,公比为 根据
根据 是
是 的等差中项,则
的等差中项,则
 ,又因为
,又因为 ,可得
,可得 ,
, ,
,
 解之得
解之得 或
或 又数列
又数列 单调递增
单调递增 
 ,
, ,
, 数列
数列 的通项公式为
的通项公式为 ;第二步
;第二步
 ,
,
 ,下面利用错位相减法求和
,下面利用错位相减法求和
 ,
,
两式相减,得 下面解不等式
下面解不等式
即 ,即
,即 ,
,
 从而
从而 故正整数
故正整数 的最最小值为5.
的最最小值为5.
试题解析: (1)设等比数列 的首项为
的首项为 ,公比为
,公比为 依题意,有
依题意,有 ,代入
,代入 ,可得
,可得 ,
, ,
,
 解之得
解之得 或
或 又数列
又数列 单调递增,
单调递增, 
 ,
, ,
, 数列
数列 的通项公式为
的通项公式为 6
6
(2)
 ,
,
 ,
,
 ,
,
两式相减,得
 即
即 ,即
,即

 从而
从而 故正整数
故正整数 的最小值为5.
的最小值为5.
 使
使 成立的正整数
成立的正整数 的最小值为5. 12分
的最小值为5. 12分
考点: 1.等差数列与等比数列的通项公式;2.错位相减法求数列的和;3.解不等式

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如右数据:
| 单价 | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
| 销量 | 90 | 84 | 83 | 80 | 75 | 68 |
由表中数据,求得线性回归方程为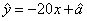 .若在这些样本点中任取一点,则它在回归直线左下方的概率为_______.
.若在这些样本点中任取一点,则它在回归直线左下方的概率为_______.
 的周长为
的周长为 ,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为 .
,把它沿图中的虚线折成正六棱柱,当这个正六棱柱的体积最大时,它的外接球的表面积为 .
 (元)
(元) (件)
(件) 的图象大致是( ).
的图象大致是( ).
 ”是“曲线
”是“曲线 为双曲线”的
为双曲线”的 的一条渐近线为
的一条渐近线为 ,则它的离心率为
,则它的离心率为 B.
B. C.
C. D.
D.
 ,那么输出的a值为( )
,那么输出的a值为( ) B.
B. C.
C. D.
D.

 B.f(x)=
B.f(x)= C.f(x)=-tanx D.f(x)=
C.f(x)=-tanx D.f(x)=