题目内容
在正项等比数列 中,公比
中,公比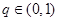 ,
, 且
且 和
和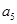 的等比中项是
的等比中项是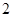 .
.
(1)求数列 的通项公式;
的通项公式;
(2)若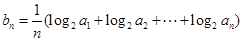 ,判断数列
,判断数列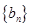 的前
的前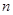 项和
项和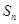 是否存在最大值,若存在,求出使
是否存在最大值,若存在,求出使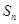 最大时
最大时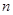 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(1) ;(2)存在
;(2)存在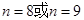 使
使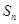 最大.
最大.
解析试题分析:(1)由 且
且 和
和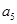 的等比中项是
的等比中项是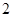 得到
得到 ,解出
,解出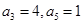 .根据
.根据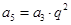 ,得到
,得到 ,又因为
,又因为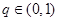 ,所以
,所以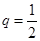 ,那么
,那么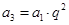 ,得到
,得到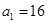 ,所以数列
,所以数列 通项公式是
通项公式是 ;(2)由对数的运算
;(2)由对数的运算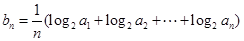
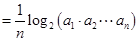 ,由于
,由于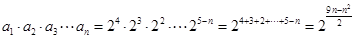 ,所以
,所以 ,所以
,所以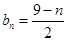 ,那么数列
,那么数列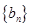 是以首项为
是以首项为 ,公差为
,公差为 的等差数列,那么
的等差数列,那么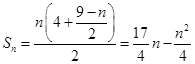 ,所以当
,所以当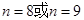 使
使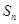 最大.
最大.
试题解析:(1)解:依题意: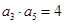 ,
,
又 ,且公比
,且公比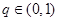 ,
,
解得  。
。
∴  ,
,
∴ 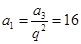
∴ 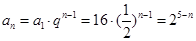 .
.
(2)∵ 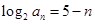 ,
,
∴ 
∵当 时,
时,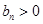 ,当
,当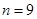 时,
时,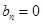 ,当
,当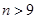 时,
时,
∴ 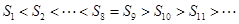 .
.
∴ 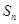 有最大值,此时
有最大值,此时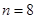 或
或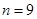 .
.
考点:等比数列;数列不等式.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案
相关题目
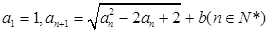
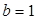 ,求
,求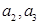 及数列
及数列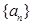 的通项公式;
的通项公式;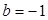 ,问:是否存在实数
,问:是否存在实数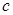 使得
使得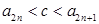 对所有
对所有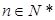 成立?证明你的结论.
成立?证明你的结论.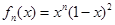 在
在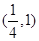 上的最大值为
上的最大值为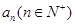
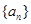 的通项公式;
的通项公式;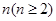 ,都有
,都有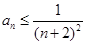 ;
;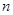 项和
项和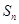 ,求证:对任何正整数
,求证:对任何正整数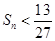 成立
成立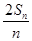 =an+1-
=an+1- n2-n-
n2-n-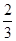 ,n∈N*.
,n∈N*.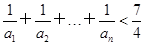 .
. 满足:
满足: ,且
,且 ,
,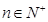 .
.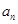 ;
;
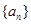 的首项
的首项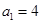 ,公差
,公差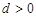 ,且
,且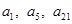 分别是正数等比数列
分别是正数等比数列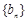 的
的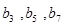 项.
项.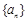 与
与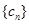 对任意
对任意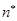 均有
均有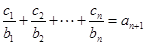 成立,设
成立,设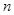 项和为
项和为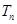 ,求
,求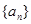 满足:
满足: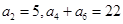 ,
,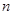 项和为
项和为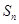 .
.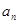 及
及 ,求数列
,求数列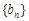 的前
的前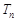 .
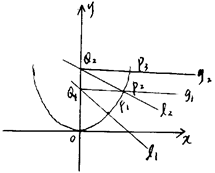
.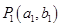 是曲线C:
是曲线C: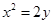 上的一点(其中
上的一点(其中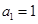 ),过点
),过点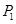 作与曲线C在
作与曲线C在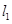 交
交 轴于点
轴于点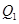 ,过
,过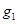 与曲线C在第一象限交于点
与曲线C在第一象限交于点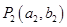 ;再过点
;再过点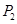 处的切线垂直的直线
处的切线垂直的直线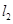 交轴于点
交轴于点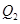 ,过
,过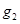 与曲线C在第一象限交于点
与曲线C在第一象限交于点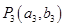 ;如此继续下去,得一系列的点
;如此继续下去,得一系列的点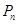 、。(其中
、。(其中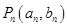 )
)
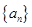 的通项公式。
的通项公式。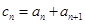 ,且
,且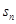 是数列
是数列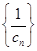 的前
的前 项和,
项和,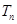 是数列
是数列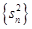 的前
的前 的前n项和
的前n项和 ,已知对任意的
,已知对任意的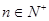 ,点
,点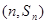 均在函数
均在函数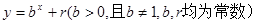 的图像上.
的图像上.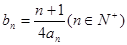 ,求数列
,求数列 的前n项和
的前n项和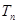 .
.