题目内容
如图一,△ABC是正三角形,△ABD是等腰直角三角形,AB=BD=2。将△ABD沿边AB折起, 使得△ABD与△ABC成直二面角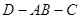 ,如图二,在二面角
,如图二,在二面角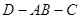 中.
中.
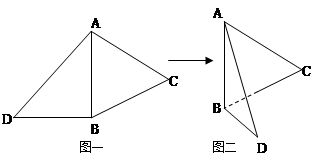
(1)求证:BD⊥AC;
(2)求D、C之间的距离;
(3)求DC与面ABD成的角的正弦值。
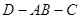 ,如图二,在二面角
,如图二,在二面角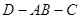 中.
中.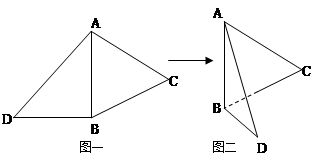
(1)求证:BD⊥AC;
(2)求D、C之间的距离;
(3)求DC与面ABD成的角的正弦值。
(1)根据线面垂直的性质定理来得到线线垂直的证明。关键的一步是利用面ABD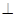 面ABC,得到
面ABC,得到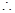 BD
BD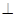 面ABC,加以证明。
面ABC,加以证明。
(2) 2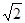 (3)
(3)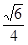
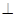 面ABC,得到
面ABC,得到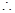 BD
BD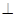 面ABC,加以证明。
面ABC,加以证明。(2) 2
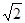 (3)
(3)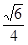
试题分析: 解:(1)依题意,面ABD
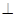 面ABC,AB是交线,
面ABC,AB是交线,而BD
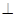 AB,
AB,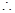 BD
BD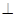 面ABC,又AC
面ABC,又AC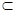 面ABC,
面ABC,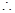 BD⊥AC; 4分
BD⊥AC; 4分(2)由(1)知,BD面ABC,而BC
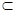 面ABC,
面ABC,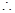 BD⊥BC;Rt
BD⊥BC;Rt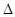 DBC中,BC=BA=2,BD=2,
DBC中,BC=BA=2,BD=2,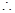 DC=
DC=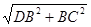 =
=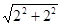 =2
=2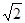 ; 8分
; 8分(3)取AB的中点H,连CH、DH和DC,

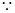 △ABC是正三角形,
△ABC是正三角形,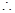 CH
CH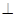 AB,又
AB,又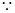 面ABC
面ABC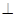 面ABD,
面ABD,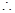 CH
CH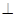 面ABD,
面ABD, DH是DC在面ABD内的射影,
DH是DC在面ABD内的射影,
 CDH是DC与面ABD成的角。
CDH是DC与面ABD成的角。而CH=
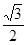 BC=
BC=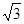 ,由(2)DC=2
,由(2)DC=2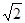 ,
, sin
sin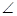 CDH=
CDH=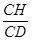 =
=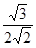 =
=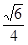 即为所求。 12分
即为所求。 12分点评:解决该试题的关键是熟练的运用判定定理和性质定理得到垂直的证明,以及角的求解,属于基础题。

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
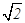 ,
,
 为两两不重合的平面,
为两两不重合的平面, 为两两不重合的直线,给出下列四个命题:
为两两不重合的直线,给出下列四个命题: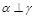 ,
, ,则
,则 ;
; ,
, ,
, ,
, ,则
,则 ;
; ,
, ,则
,则 ;
; ,
, ,
, ,
, ,则
,则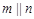 其中真命
其中真命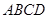 与等腰直角三角形
与等腰直角三角形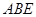 所在的平面互相垂直.
所在的平面互相垂直.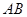 ∥
∥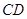 ,
,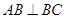 ,
,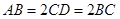 ,
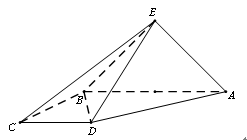
,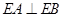 .
.
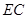 与平面
与平面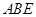 所成角的正弦值;
所成角的正弦值;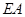 上是否存在点
上是否存在点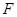 ,使
,使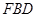 ?若存在,求出
?若存在,求出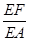 ;若不存在,说明理由.1
;若不存在,说明理由.1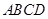 与正三角形
与正三角形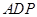 所在的平面相互垂直,且
所在的平面相互垂直,且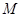 、
、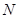
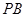 、
、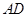 中点.
中点.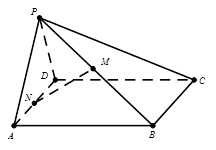
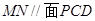 ;
;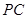 与平面
与平面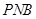 所成角的正弦值.
所成角的正弦值.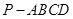 的底面为等腰梯形,
的底面为等腰梯形,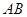 ∥
∥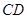 ,
,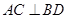 ,垂足为
,垂足为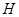 ,
,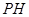 是四棱锥的高。
是四棱锥的高。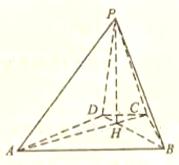
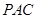
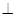 平面
平面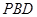 ;
;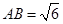 ,
,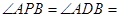 60°,求四棱锥
60°,求四棱锥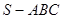 中,
中,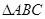 是边长为4的正三角形,
是边长为4的正三角形,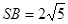 ,
,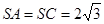 ,
,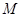 、
、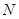 分别是
分别是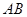 、
、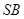 的中点;
的中点;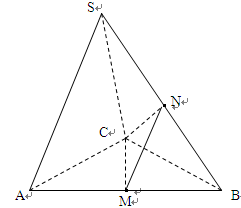
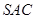
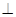 平面
平面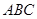 ;
;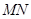 与平面
与平面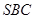 所成角的正弦值。
所成角的正弦值。