题目内容
已知展开式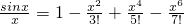 +…对x∈R且x≠0恒成立,方程
+…对x∈R且x≠0恒成立,方程 =0有无究多个根:±π,±2π,…±nπ,…,则1-
=0有无究多个根:±π,±2π,…±nπ,…,则1-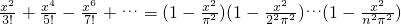 …,比较两边x2的系数可以推得1+
…,比较两边x2的系数可以推得1+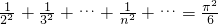 .设代数方程1-a1x2+a2x4-…+(-1)nanx2n=0有2n个不同的根:±x1,±x2,…±xn,类比上述方法可得a1=________.(用x1,x2,…,xn表示)
.设代数方程1-a1x2+a2x4-…+(-1)nanx2n=0有2n个不同的根:±x1,±x2,…±xn,类比上述方法可得a1=________.(用x1,x2,…,xn表示)
(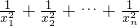 )
)
分析:由已知中式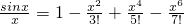 +…对x∈R且x≠0恒成立,方程
+…对x∈R且x≠0恒成立,方程 =0有无究多个根:±π,±2π,…±nπ,…,则,1-
=0有无究多个根:±π,±2π,…±nπ,…,则,1-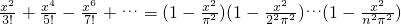 …,比较两边x2的系数可以推得1+
…,比较两边x2的系数可以推得1+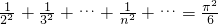 .类比推理可由代数方程1-a1x2+a2x4-…+(-1)nanx2n=0有2n个不同的根:±x1,±x2,…±xn,转化 为1-a1x2+a2x4-…+(-1)nanx2n=
.类比推理可由代数方程1-a1x2+a2x4-…+(-1)nanx2n=0有2n个不同的根:±x1,±x2,…±xn,转化 为1-a1x2+a2x4-…+(-1)nanx2n=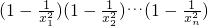 ,比较两边x2的系数即可得到答案.
,比较两边x2的系数即可得到答案.
解答:由1-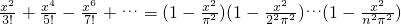 中,
中,
比较两边x2的系数可以推得:1+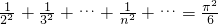 .
.
类比揄代数方程1-a1x2+a2x4-…+(-1)nanx2n=0有2n个不同的根:±x1,±x2,…±xn,
即1-a1x2+a2x4-…+(-1)nanx2n=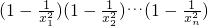 中,
中,
比较两边x2的系数可以推得:a1=( )
)
故答案为:( )
)
点评:本题考查的知识点是类比推理,其中由已知根据方程根的形式,将一个累加式变成一个累乘式,用到一次类比推理;现时观察两边x2的系数得到结论,又用到一次类比,故难较大.
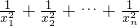 )
)分析:由已知中式
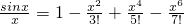 +…对x∈R且x≠0恒成立,方程
+…对x∈R且x≠0恒成立,方程 =0有无究多个根:±π,±2π,…±nπ,…,则,1-
=0有无究多个根:±π,±2π,…±nπ,…,则,1-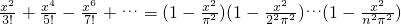 …,比较两边x2的系数可以推得1+
…,比较两边x2的系数可以推得1+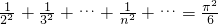 .类比推理可由代数方程1-a1x2+a2x4-…+(-1)nanx2n=0有2n个不同的根:±x1,±x2,…±xn,转化 为1-a1x2+a2x4-…+(-1)nanx2n=
.类比推理可由代数方程1-a1x2+a2x4-…+(-1)nanx2n=0有2n个不同的根:±x1,±x2,…±xn,转化 为1-a1x2+a2x4-…+(-1)nanx2n=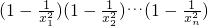 ,比较两边x2的系数即可得到答案.
,比较两边x2的系数即可得到答案.解答:由1-
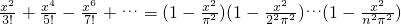 中,
中,比较两边x2的系数可以推得:1+
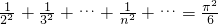 .
.类比揄代数方程1-a1x2+a2x4-…+(-1)nanx2n=0有2n个不同的根:±x1,±x2,…±xn,
即1-a1x2+a2x4-…+(-1)nanx2n=
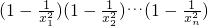 中,
中,比较两边x2的系数可以推得:a1=(
 )
)故答案为:(
 )
)点评:本题考查的知识点是类比推理,其中由已知根据方程根的形式,将一个累加式变成一个累乘式,用到一次类比推理;现时观察两边x2的系数得到结论,又用到一次类比,故难较大.

练习册系列答案
相关题目
 展开式的各项依次记为a1(x),a2(x),a3(x),…an(x),an+1(x).
展开式的各项依次记为a1(x),a2(x),a3(x),…an(x),an+1(x). 展开式的各项依次记为a1(x),a2(x),a3(x),…an(x),an+1(x).
展开式的各项依次记为a1(x),a2(x),a3(x),…an(x),an+1(x).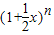 展开式的各项依次记为a1(x),a2(x),a3(x),…an(x),an+1(x).
展开式的各项依次记为a1(x),a2(x),a3(x),…an(x),an+1(x).