题目内容
某地最近十年粮食需求量逐年上升,下表是部分统计数据:| 年份 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 |
| 需求量(万吨) | 3 | 6 | 5 | 7 | 8 |
(Ⅱ)利用(Ⅰ)中所求出的直线方程预测该地第6年的粮食需求量.
分析:(I)由所给数据看出,年需求量与年份之间是近似直线上升,做出平均数,利用最小二乘法做出b,a,写出线性回归方程.
(II)把所给的x的值代入线性回归方程,求出变化以后的预报值,得到结果.
(II)把所给的x的值代入线性回归方程,求出变化以后的预报值,得到结果.
解答:解:(I)由所给数据看出,年需求量与年份之间是近似直线上升,下面来求回归直线方程:
=
=3,
=
=5.8,
∴b=
=1.1,
∴a=5.8-3×1.1=2.5,
∴线性回归方程是y=1.1x-2.5;
(II)可预测第6年的粮食需求量为y=1.1×6+2.5=9.1万吨).
. |
| x |
| 1+2+3+4+5 |
| 5 |
. |
| y |
| 3+6+5+7+8 |
| 5 |
∴b=
| 1×3+2×6+3×5+4×7+5×8-5×3×5.8 |
| 12+22+32+42+52-5×32 |
∴a=5.8-3×1.1=2.5,
∴线性回归方程是y=1.1x-2.5;
(II)可预测第6年的粮食需求量为y=1.1×6+2.5=9.1万吨).
点评:本题考查回归分析的基本思想及其初步应用,考查回归方程的意义和求法,考查数据处理的基本方法和能力,考查利用统计思想解决实际问题的能力.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
某地最近十年粮食需求量逐年上升,下表是部分统计数据:
(Ⅰ)利用所给数据求年需求量与年份之间的回归直线方程
=bx+a;
(Ⅱ)利用(Ⅰ)中所求的直线方程预测该地2012年的粮食需求量.
| 年份 | 2002 | 2004 | 2006 | 2008 | 2010 |
| 需求量(万吨) | 236 | 246 | 257 | 276 | 286 |
| ? |
| y |
(Ⅱ)利用(Ⅰ)中所求的直线方程预测该地2012年的粮食需求量.
(本小题满分10分)
某地最近十年粮食需求量逐年上升, 下表是
下表是 部分统计数据:
部分统计数据:
| 年份 | 2002 | 2004 | 2006 | 2008 | 2010 |
| 需求量(万吨) | 236 | 246 | 257 | 276 | 286 |
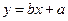 ;
;
某地最近十年粮食需求量逐年上升,下表是统计数据:
(I) 利用所给数据求年需量与年份之间的回归直线方程 =bx+a;
=bx+a;
(II)利用(I)中所求出的直线方程预测该地2013年的粮食需求量.
| 年份 | 2003 | 2005 | 2007 | 2009 | 2011 |
| 需求量(万吨) | 236 | 246 | 257 | 276 | 286 |
 =bx+a;
=bx+a;(II)利用(I)中所求出的直线方程预测该地2013年的粮食需求量.
