题目内容
【题目】如图半圆柱
的底面半径和高都是1，面
是它的轴截面（过上下底面圆心连线
的平面），
分别是上下底面半圆周上一点.
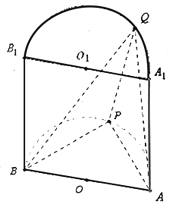
（1）证明：三棱锥
体积
，并指出
和
满足什么条件时有
（2）求二面角
平面角的取值范围，并说明理由.
【答案】（1）见解析（2）
【解析】试题分析：
(1)利用题意结合均值不等式讨论即可得出结论：需要
.
(2)利用题意建立空间直角坐标系，然后求得
的表达式即可确定二面角
平面角的取值范围.
试题解析：
（1）
证明： 
，其中
是
到平面
的距离，（由条件及圆柱性质）即平面
到
的距离且为定值1
由半圆性质
所以
所以由均值不等式
要有
因为
等价于要有
面
所以需要
即可！
注：1、不用均值不等式证明老师斟酌给分，若数形结合证明，只要说清楚了就给满分2、（
等价说法： 
， 
面
都可以！）
（2）
如图以
为原点、
为
轴、
为
轴建坐标系作
垂直于平面
于
，
记
平面
法向量可取
设平面
的法向量
得
可令
所以二面角
平面角范围
练习册系列答案
阅读快车系列答案
相关题目
