题目内容
已知向量p//q,其中![]() ,
,![]() R且
R且![]() >0,
>0,![]() ,把其中
,把其中![]() ,
,![]() 所满足的关系式记为
所满足的关系式记为![]() ,若函数
,若函数![]() 为奇函数,且当
为奇函数,且当![]() >0时,
>0时,![]() 有最小值
有最小值![]() .
.
(1)求函数![]() 的表达式;
的表达式;
(2)设数列![]() 满足如下关系:
满足如下关系:![]() N*),且
N*),且
![]() ,求数列
,求数列![]() 的通项公式,并求数列
的通项公式,并求数列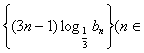 N*)前
N*)前![]() 项的和S
项的和S![]() .
.
解:(1)由p//q,得![]() ,
,
∴![]()
又函数![]() 为奇函数,有
为奇函数,有![]() ,可得
,可得![]()
当![]() ,
,![]()
∴![]() ,∴
,∴![]()
故![]() .
.
(2)
![]() ,
,


∴![]() .
.
∴![]() ,∴
,∴ N*).
N*).
∴数列 的通项为
的通项为![]() .
.
∴![]() ①
①
∴![]() ②
②
①-②,得![]()
∴![]() ∈N*).
∈N*).

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目
已知向量
、
的模都是2,其夹角为60°,又知
=3
+2
,
=
+3
,则P、Q两点间的距离为( )
| a |
| b |
| OP |
| a |
| b |
| OQ |
| a |
| b |
A、2
| ||
B、
| ||
C、2
| ||
D、
|
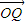 =t
=t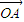 +(1-t)
+(1-t)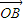 (t∈R,t≠0)
(t∈R,t≠0) 时,设动点Q关于X轴的对称点为点P,直线PD交轨迹E于点R (异于P点),试问:直线QR与X轴的交点是否为定点,若是定点,求出其坐标;若不是定点,请说明理由.
时,设动点Q关于X轴的对称点为点P,直线PD交轨迹E于点R (异于P点),试问:直线QR与X轴的交点是否为定点,若是定点,求出其坐标;若不是定点,请说明理由.