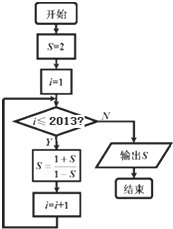
题目内容
方程sinx+
cosx=1在闭区间[0，2π]上的所有解的和等于 ．
| 3 |
考点：两角和与差的正弦函数,正弦函数的图象
专题：三角函数的求值
分析：由三角函数公式可得sin（x+
）=
，可知x+
=2kπ+
，或x+
=2kπ+
，k∈Z，结合x∈[0，2π]，可得x值，求和即可．
| π |
| 3 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| 5π |
| 6 |
解答：
解：∵sinx+
cosx=1，
∴
sinx+
cosx=
，
即sin（x+
）=
，
可知x+
=2kπ+
，或x+
=2kπ+
，k∈Z，
又∵x∈[0，2π]，
∴x=
，或x=
，
∴
+
=
故答案为：
．
| 3 |
∴
| 1 |
| 2 |
| ||
| 2 |
| 1 |
| 2 |
即sin（x+
| π |
| 3 |
| 1 |
| 2 |
可知x+
| π |
| 3 |
| π |
| 6 |
| π |
| 3 |
| 5π |
| 6 |
又∵x∈[0，2π]，
∴x=
| 11π |
| 6 |
| π |
| 2 |
∴
| 11π |
| 6 |
| π |
| 2 |
| 7π |
| 3 |
故答案为：
| 7π |
| 3 |
点评：本题考查两角和与差的三角函数公式，属基础题．
练习册系列答案
相关题目
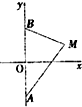已知点A、B的坐标分别是（0，-1），（0，1），直线AM、BM相交于点M，且它们的斜率之积为-