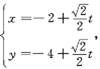题目内容
已知曲线C: ![]() , 过点Q
, 过点Q![]() 作C的切线
作C的切线![]() , 切点为P.
, 切点为P.
(1) 求证:不论![]() 怎样变化, 点P总在一条定直线上;
怎样变化, 点P总在一条定直线上;
(2) 若![]() , 过点P且与
, 过点P且与![]() 垂直的直线与
垂直的直线与![]() 轴交于点T, 求
轴交于点T, 求![]() 的最小值(O为原点).
的最小值(O为原点).
命题意图![]() 本题主要考查导数的几何意义以及函数切线方程的求法。
本题主要考查导数的几何意义以及函数切线方程的求法。
知识依托![]() 导数的几何意义,直线方程的形式,基本不等式
导数的几何意义,直线方程的形式,基本不等式
错解分析![]() 对题中的数据的实际意义不理解,以及基本不等式中的第三个条件等号成立时要满足条件没有讨论。
对题中的数据的实际意义不理解,以及基本不等式中的第三个条件等号成立时要满足条件没有讨论。
技巧与方法![]() 直接利用导数的几何意义求切线的斜率;在第(2)小题中,把y表示成x的函数代入
直接利用导数的几何意义求切线的斜率;在第(2)小题中,把y表示成x的函数代入![]() 并利用基本不等式求最小值。
并利用基本不等式求最小值。
解: (1)设P点坐标为![]() , 则
, 则![]() 由
由![]() 则以P点为切点
则以P点为切点
的切线斜率为![]() 若
若![]() 则
则![]() 不符合题意.
不符合题意.
∵切线过点![]() , ∴斜率为
, ∴斜率为![]() .
.
∴![]() , ∴
, ∴![]() , ∴切点P总在直线
, ∴切点P总在直线![]()
![]() 上.
上.
(2) 解法一: ∵l的斜率为![]() ,∴PT的斜率为
,∴PT的斜率为![]() ,
,
∴PT的方程为![]() .
.
令![]() ,得PT与x轴交点的横坐标为
,得PT与x轴交点的横坐标为![]() .
.
在(1)中, ![]() , 又
, 又![]() ∴
∴![]() . ∴
. ∴![]()
∴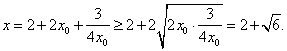
(当且仅当![]() , 即
, 即![]() 时等号成立). ∴
时等号成立). ∴![]() 的最小值为
的最小值为![]() .
.
解法二:直线l的斜率为![]() , 则垂线斜率为
, 则垂线斜率为![]() ,
,
垂线方程为![]() .
.
令![]() , 解得与x轴的交点T的横坐标为
, 解得与x轴的交点T的横坐标为
![]()
当且仅当3![]() ,即
,即![]() 时, 等号成立. ∴
时, 等号成立. ∴![]() 的最小值为
的最小值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图:已知曲线C:在点P(1,1)处的切线与x轴交于点Q1,再过Q1点作x轴的垂线交曲线C于点P1,再过P1作C的切线与x轴交于点Q2,依次重复下去,过Pn(xn,yn)作C的切线与x轴交于点Qn(xn+1,O).
如图:已知曲线C:在点P(1,1)处的切线与x轴交于点Q1,再过Q1点作x轴的垂线交曲线C于点P1,再过P1作C的切线与x轴交于点Q2,依次重复下去,过Pn(xn,yn)作C的切线与x轴交于点Qn(xn+1,O).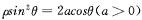 ,过点P(-2,-4)的直线l的参数方程为:
,过点P(-2,-4)的直线l的参数方程为: