题目内容
6.求函数y=$\sqrt{3}$cos(x+10°)-sin(x+70°)的值域.分析 将x+70°拆成(x+10°)+60°使用两角和的正弦公式展开合并化简即可.
解答 解:y=$\sqrt{3}$cos(x+10°)-sin(x+10°+60°)
=$\sqrt{3}$cos(x+10°)-$\frac{1}{2}$sin(x+10°)-$\frac{\sqrt{3}}{2}$cos(x+10°)
=$\frac{\sqrt{3}}{2}$cos(x+10°)-$\frac{1}{2}$sin(x+10°)
=cos(x+10°+30°).
=cos(x+40°).
∴y=$\sqrt{3}$cos(x+10°)-sin(x+70°)的值域是[-1,1].
点评 本题考查了三角函数的化简,观察两角的关系,数列掌握三角公式是解题关键.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
1.已知非零向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$+$\overrightarrow{b}$|=|$\overrightarrow{a}$$-\overrightarrow{b}$|=3|$\overrightarrow{b}$|,则cos<$\overrightarrow{a}$,$\overrightarrow{b}$$-\overrightarrow{a}$>=( )
| A. | $\frac{2\sqrt{2}}{3}$ | B. | $\frac{1}{3}$ | C. | -$\frac{2\sqrt{2}}{3}$ | D. | -$\frac{1}{3}$ |
11.$\underset{lim}{n→∞}$$\frac{{1}^{p}{+2}^{p}{+3}^{p}+…{+n}^{p}}{{n}^{p+1}}$(p>0)可表示成定积分( )
| A. | ${∫}_{0}^{1}$$\frac{1}{x}$dx | B. | ${∫}_{0}^{1}$xpdx | C. | ${∫}_{0}^{1}$($\frac{1}{x}$)pdx | D. | ${∫}_{0}^{1}$($\frac{x}{n}$)pdx |
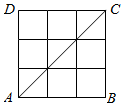 如图,ABCD为边长为3的正方形,把各边三等分后,共有16个交点,从中选取两个交点作为向量,则与$\overrightarrow{AC}$平行且长度为2$\sqrt{2}$的向量个数有8个.
如图,ABCD为边长为3的正方形,把各边三等分后,共有16个交点,从中选取两个交点作为向量,则与$\overrightarrow{AC}$平行且长度为2$\sqrt{2}$的向量个数有8个.