题目内容
（09年西城区抽样文）（14分）
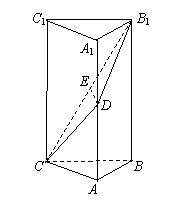
如图，在直三棱柱
中，
，D、E分别是AA1、B1C的中点.
(Ⅰ) 求证：
平面
；
(Ⅱ) 求异面直线
与
所成角的大小；
(Ⅲ) 求二面角C-B1D-B的大小.
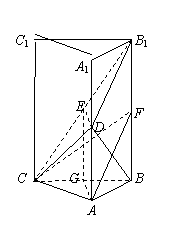
解析：方法一：（Ⅰ）证明：如图，设G为BC的中点，连接EG，AG，
在
中，
，
，且
，
又
，且
，
，
四边形
为平行四边形，
， ------------------------2分
又
平面ABC，
平面ABC，
平面
. --------------------------4分
（Ⅱ）解：如图，设F为BB1的中点，连接AF，CF，
直三棱柱
，且D是AA1的中点，
，
为异面直线
与
所成的角或其补角. -------------------7分
在Rt
中，
，AB=1，BF=1，
，同理
，
在
中，
，
在
中，
，
.
异面直线
与
所成的角为
. ----------------------9分
（Ⅲ）解：直三棱柱，
，
又
，
平面
. ----------------------10分
如图，连接BD，
在
中，
，
，即
，
是CD在平面内的射影，
，
为二面角C-B1D-B的平面角. --------------------12分
在
中, 
, BC=1, 
，
,
二面角C-B1D-B的大小为
. --------------------14分
方法二：（Ⅰ）同方法一. ----------------------4分
（Ⅱ）如图，以B为原点，BC、BA、BB1分别为x、y、z轴，建立空间直角坐标系O-xyz，
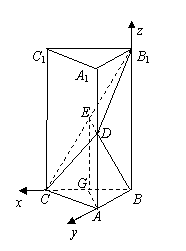
则
，
, ----------------------6分
，
异面直线与所成的角为. ----------------------9分
（Ⅲ）解：直三棱柱，，
又，
平面. ---------------------------10分
如图，连接BD，
在中，，
，即，
是CD在平面内的射影，
，
为二面角C-B1D-B的平面角. -----------------------12分
，
，
二面角C-B1D-B的大小为
. ------------------------14分
R).
的单调区间；
处切线的斜率都小于2a2，求a的取值范围.
.
的值域和最小正周期；
，且
，求
的值.
. 现两人玩射击游戏，规则如下：若某人某次射击击中目标，则由他继续射击，否则由对方接替射击. 甲、乙两人共射击3次，且第一次由甲开始射击. 假设每人每次射击击中目标与否均互不影响.
，F是C的焦点，过点F的直线l与C相交于A、B两点，O为坐标原点.
，求直线l的方程.
R)在其图象上一点A
处切线的斜率为-1.