题目内容
(09年西城区抽样文)(14分)
给定抛物线![]() ,F是C的焦点,过点F的直线l与C相交于A、B两点,O为坐标原点.
,F是C的焦点,过点F的直线l与C相交于A、B两点,O为坐标原点.
(Ⅰ)设l的斜率为1,求以AB为直径的圆的方程;
(Ⅱ)设![]() ,求直线l的方程.
,求直线l的方程.
解析:方法一:(Ⅰ)解:由题意,得![]() ,直线l的方程为
,直线l的方程为![]() .
.
由![]() , 得
, 得![]() ,
,
设A, B两点坐标为![]() , AB中点M的坐标为
, AB中点M的坐标为![]() ,
,
则![]() ,
,
故点![]() -----------3分
-----------3分
所以![]() ,
,
故圆心为![]() , 直径
, 直径![]() ,
,
所以以AB为直径的圆的方程为![]() ; -----------6分
; -----------6分
(Ⅱ)解:因为![]() , 三点A, F, B共线且点A, B在点F两侧,
, 三点A, F, B共线且点A, B在点F两侧,
所以![]() ,
,
设A, B两点坐标为![]() , 则
, 则![]() ,
,
所以![]() 1
1
因为点A, B在抛物线C上,
所以![]() , 2 ---------10分
, 2 ---------10分
由12,解得
所以![]() , -------------13分
, -------------13分
故直线l的方程为![]() 或
或![]() .-----------14分
.-----------14分
方法二:(Ⅰ)解:由题意,得![]() ,直线l的方程为
,直线l的方程为![]() .
.
由![]() , 得
, 得![]() ,
,
设A, B两点坐标为![]() , AB中点M的坐标为
, AB中点M的坐标为![]() ,
,
因为![]() 所以
所以![]() ,
,
所以![]() , 故圆心为
, 故圆心为![]() , --------------3分
, --------------3分
由抛物线定义,得![]() ,
,
所以![]() (其中p=2).
(其中p=2).
所以以AB为直径的圆的方程为![]() ; ---------------6分
; ---------------6分
(Ⅱ)解:因为![]() , 三点A, F, B共线且点A, B在点F两侧,
, 三点A, F, B共线且点A, B在点F两侧,
所以![]() ,
,
设A, B两点坐标为![]() , 则
, 则![]() ,
,
所以![]() 1 -----------------9分
1 -----------------9分
设直线AB的方程为![]() 或
或![]() (不符合题意,舍去).
(不符合题意,舍去).
由![]() ,消去x得
,消去x得 ![]() ,
,
因为直线l与C相交于A, B两点,所以![]() ,
,
则![]() ,
, ![]() , 2
, 2
由12,得方程组 ,解得
,解得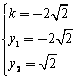 或
或  ,---13分
,---13分

 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案