题目内容
在 中,角
中,角 所对边分别为
所对边分别为 ,已知
,已知 ,且最长边的边长为
,且最长边的边长为 .求:
.求:
(1)角 的正切值及其大小;
的正切值及其大小;
(2) 最短边的长.
最短边的长.
(1)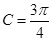 ;(2)最短边为
;(2)最短边为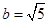 .
.
解析试题分析:(1)先用诱导公式转化: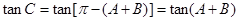 ,然后利用两角和的正切公式进行计算,得到
,然后利用两角和的正切公式进行计算,得到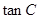 的值,结合
的值,结合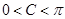 与特殊角的三角函数值可得到角
与特殊角的三角函数值可得到角 ;(2)先结合(1)中所求得的角
;(2)先结合(1)中所求得的角 及
及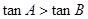 ,判断出最小的角为
,判断出最小的角为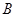 ,故最小的边为
,故最小的边为 ,最长边为
,最长边为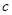 ,然后计算出
,然后计算出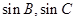 ,再由正弦定理:
,再由正弦定理: 可计算出最小边
可计算出最小边 的值.
的值.
试题解析:(1)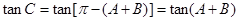
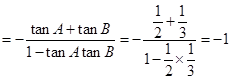 4分
4分
∵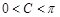 ,∴
,∴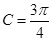 6分
6分
(2)∵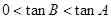 ,∴
,∴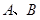 均为锐角,则
均为锐角,则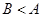 ,又
,又 为钝角
为钝角
∴最短边为 ,最长边长为
,最长边长为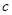 8分
8分
由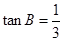 ,解得
,解得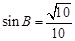 10分
10分
由 ,∴
,∴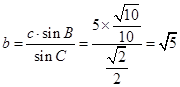 13分.
13分.
考点:1.诱导公式;2.两角和的正切公式;3.同角三角函数的基本关系式;4.正弦定理.

练习册系列答案
相关题目
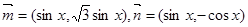 ,设函数
,设函数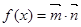 ,若函数
,若函数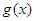 的图象与
的图象与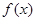 的图象关于坐标原点对称.
的图象关于坐标原点对称. 上的最大值,并求出此时
上的最大值,并求出此时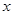 的取值;
的取值;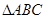 中,
中,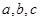 分别是角
分别是角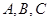 的对边,若
的对边,若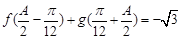 ,
,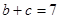 ,
,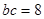 ,求边
,求边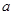 的长.
的长. ,求
,求 的值.
的值. (其中C为锐角).
(其中C为锐角). 中,
中,  分别是角
分别是角 的对边,且
的对边,且 .
. 的大小; (2)若
的大小; (2)若 ,
, ,求
,求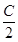 +ccos2
+ccos2 =
= b.
b.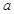 ,
, ,
, 分别是
分别是 的三个内角
的三个内角 ,
, ,
, 所对的边,若
所对的边,若 ,
, ,
, ,求边
,求边 ),n=
),n= ,且m∥n
,且m∥n ,BC=1,P为△ABC内一点,∠BPC=90°.
,BC=1,P为△ABC内一点,∠BPC=90°.
 ,求PA;
,求PA;