题目内容
“数列{an}为常数列”是“数列{an}既是等差数列又是等比数列”的
- A.充分不必要条件
- B.必要不充分条件
- C.充要条件
- D.既不充分也不必要条件
B
分析:先证明必要性:若{an}是常数列,如果an≠0,可得数列{an}是等差数列,若{an}既是等差数列又是等比数列,根据等比数列和等差数列的性质进行求解;
解答:数列{an}为常数列,如果an=0,则数列{an}不是等比数列;
显然数列{an}是以a为首项,以0为公差的等差数列,且{an}是以a为首项,以1为公比的等比数列.
若{an}既是等差数列又是等比数列,则对任意n∈N*都有:
 可得
可得 =anan+2,整理得(an-an+2)2=0,
=anan+2,整理得(an-an+2)2=0,
∴an=an+2=an+1.
∴{an}是常数列.
∴“数列{an}既是等差数列又是等比数列”?数列{an}为常数列”
∴“数列{an}为常数列”是“数列{an}既是等差数列又是等比数列”的必要不充分条件,
故选B;
点评:此题主要考查等比数列和等差数列的性质及其应用,利用特殊值法进行求解,是一道基础题;
分析:先证明必要性:若{an}是常数列,如果an≠0,可得数列{an}是等差数列,若{an}既是等差数列又是等比数列,根据等比数列和等差数列的性质进行求解;
解答:数列{an}为常数列,如果an=0,则数列{an}不是等比数列;
显然数列{an}是以a为首项,以0为公差的等差数列,且{an}是以a为首项,以1为公比的等比数列.
若{an}既是等差数列又是等比数列,则对任意n∈N*都有:
 可得
可得 =anan+2,整理得(an-an+2)2=0,
=anan+2,整理得(an-an+2)2=0,∴an=an+2=an+1.
∴{an}是常数列.
∴“数列{an}既是等差数列又是等比数列”?数列{an}为常数列”
∴“数列{an}为常数列”是“数列{an}既是等差数列又是等比数列”的必要不充分条件,
故选B;
点评:此题主要考查等比数列和等差数列的性质及其应用,利用特殊值法进行求解,是一道基础题;

练习册系列答案
相关题目
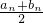 ≥0时,有[an+1,bn+1]=[an,
≥0时,有[an+1,bn+1]=[an, ≥0时,有[an+1,bn+1]=[an,
≥0时,有[an+1,bn+1]=[an, ];当
];当 <0时,有[an+1,bn+1]=[
<0时,有[an+1,bn+1]=[ ,bn].
,bn].