题目内容
(本小题共13分)设 ,已知函数
,已知函数 .
.
(1)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)若对任意的 ,有
,有 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1) 的单调递增区间为
的单调递增区间为 ,单调递减区间为(0,2); (2)
,单调递减区间为(0,2); (2) .
.
【解析】
试题分析:(1) 求函数的导数,解不等式 可得函数的递增区间,解不等式
可得函数的递增区间,解不等式 可得函数的递减区间; (2)分离参数得
可得函数的递减区间; (2)分离参数得 ,求函数
,求函数 的最小值即可.
的最小值即可.
试题解析:(1)当 时,
时, ,
,
则 ,
,
由 ,得
,得 ,或
,或 ,
,
由 ,得
,得 ,
,
所以 的单调递增区间为
的单调递增区间为 ,单调递减区间为(0,2).(6分)
,单调递减区间为(0,2).(6分)
(2)依题意,对 ,
, ,
,
这等价于,不等式 对
对 恒成立.
恒成立.
令 ,
,
则 ,
,
所以 在区间
在区间 上是减函数,
上是减函数,
所以 的最小值为
的最小值为 .
.
所以 ,即实数
,即实数 的取值范围为
的取值范围为 .(13分)
.(13分)
考点:导数与函数的单调性、极值,不等式恒成立问题.

练习册系列答案
相关题目
 +lg(2x-1)的定义域是( )
+lg(2x-1)的定义域是( ) B.
B. C.
C. D.
D.
 ,则它们的图象可能是( )
,则它们的图象可能是( )
 的最小正周期为
的最小正周期为 ,则
,则 ( )
( ) C.-1 D.
C.-1 D.
 ,且
,且 ,则
,则 的值为__________.
的值为__________. 有唯一的零点,则实数
有唯一的零点,则实数 的值为( )
的值为( ) 的虚部为__________.
的虚部为__________.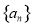 的公比为2,若
的公比为2,若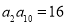 ,则
,则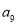 的值是
的值是