题目内容
一个多面体的直观图(正视图,侧视图,俯视图)如图所示,M,N分别为A1B,B1C1的中点,
(Ⅰ)求证:MN∥平面ACC1A1;
(Ⅱ)求证:MN⊥平面A1BC;
(Ⅲ)求二面角A-A1B-C的大小。
(Ⅰ)求证:MN∥平面ACC1A1;
(Ⅱ)求证:MN⊥平面A1BC;
(Ⅲ)求二面角A-A1B-C的大小。
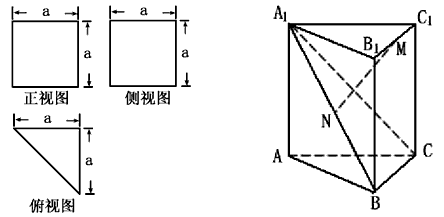
解:由题意可知,这个几何体是直三棱柱,且AC⊥BC,AC=BC=CC1,
(Ⅰ)连结AC1,AB1,
由直三棱柱的性质得,AA1⊥平面A1B1C1,所以AA1⊥A1B1,
则四边形ABB1A1为矩形,
由矩形性质得AB1过A1B的中点M,
在△AB1C1中,由中位线性质得MN∥AC1,
又AC1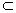 平面ACC1A1,MN
平面ACC1A1,MN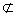 平面ACC1A1,
平面ACC1A1,
所以MN∥平面ACC1A1。
(Ⅱ)因为BC⊥平面ACC1A1,AC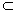 平面ACC1A1,所以BC⊥AC1,
平面ACC1A1,所以BC⊥AC1,
在正方形ACC1A1中,A1C⊥AC1,
又因为BC∩A1C=C,
所以AC1⊥平面A1BC。由MN∥AC1,得MN⊥平面A1BC。
(Ⅲ)过点C作CD⊥AB于D,
再过点D作DE⊥A1B,连接CE,
可以证明∠CED即为所求。
经计算CD=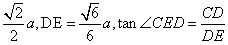 ,
,
所以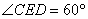 ,即二面角A-A1B-C为60°。
,即二面角A-A1B-C为60°。
(Ⅰ)连结AC1,AB1,
由直三棱柱的性质得,AA1⊥平面A1B1C1,所以AA1⊥A1B1,
则四边形ABB1A1为矩形,
由矩形性质得AB1过A1B的中点M,
在△AB1C1中,由中位线性质得MN∥AC1,
又AC1
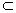 平面ACC1A1,MN
平面ACC1A1,MN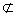 平面ACC1A1,
平面ACC1A1,所以MN∥平面ACC1A1。
(Ⅱ)因为BC⊥平面ACC1A1,AC
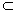 平面ACC1A1,所以BC⊥AC1,
平面ACC1A1,所以BC⊥AC1,在正方形ACC1A1中,A1C⊥AC1,
又因为BC∩A1C=C,
所以AC1⊥平面A1BC。由MN∥AC1,得MN⊥平面A1BC。
(Ⅲ)过点C作CD⊥AB于D,
再过点D作DE⊥A1B,连接CE,
可以证明∠CED即为所求。
经计算CD=
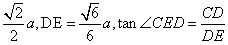 ,
,所以
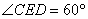 ,即二面角A-A1B-C为60°。
,即二面角A-A1B-C为60°。 
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
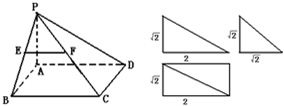 一个多面体的直观图和三视图如图所示,E,F分别为PB,PC中点.
一个多面体的直观图和三视图如图所示,E,F分别为PB,PC中点.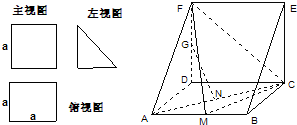
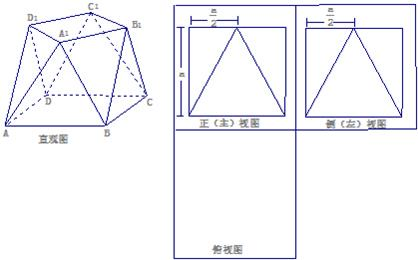 一个多面体的直观图,正(主)视图,侧(左)视图如下所示,其中正(主)视图、侧(左)视图为边长为a的正方形.
一个多面体的直观图,正(主)视图,侧(左)视图如下所示,其中正(主)视图、侧(左)视图为边长为a的正方形.
 一个多面体的直观图及三视图如图所示:(其中M、N、P、Q分别是FC、AF、DC、AD的中点)
一个多面体的直观图及三视图如图所示:(其中M、N、P、Q分别是FC、AF、DC、AD的中点)