题目内容
9. 已知函数f(x)=$\sqrt{2}$sin($\frac{5π}{4}$-2x)+1.
已知函数f(x)=$\sqrt{2}$sin($\frac{5π}{4}$-2x)+1.(1)求它的振幅、最小正周期、初相;
(2)画出函数y=f(x)在[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象.
分析 (1)由条件利用函数y=Asin(ωx+φ)的图象、性质得出结论.
(2)用五点法作函数y=Asin(ωx+φ)在一个周期上的简图.
解答 解:(1)对于函数f(x)=$\sqrt{2}$sin($\frac{5π}{4}$-2x)+1=-$\sqrt{2}$sin(-2x+$\frac{π}{4}$)+1=$\sqrt{2}$sin(2x-$\frac{π}{4}$)+1,
它的振幅为$\sqrt{2}$、最小正周期$\frac{2π}{2}$=π、初相为-$\frac{π}{4}$.
(2)由x∈[-$\frac{π}{2}$,$\frac{π}{2}$],可得2x-$\frac{π}{4}$∈[-$\frac{5π}{4}$,$\frac{3π}{4}$],用五点法做出它的图象,
列表:
| 2x-$\frac{π}{4}$ | -$\frac{5π}{4}$ | -π | -$\frac{π}{2}$ | 0 | $\frac{π}{2}$ | $\frac{3π}{4}$ |
| x | -$\frac{π}{2}$ | -$\frac{3π}{8}$ | -$\frac{π}{8}$ | $\frac{π}{8}$ | $\frac{3π}{8}$ | $\frac{π}{2}$ |
| y | 1 | 0 | -$\sqrt{2}$ | 0 | $\sqrt{2}$ | 1 |
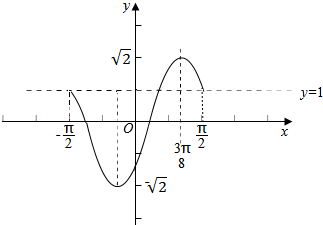
点评 本题主要考查正弦函数的图象性质,用五点法作函数函数y=Asin(ωx+φ)的一个周期上的简图,属于基础题.

练习册系列答案
相关题目
19.直线x=$\frac{2π}{3}$和x=$\frac{7π}{6}$是函数f(x)=sin(ωx+φ)(ω>0,0<φ<2π)的两条相邻的对称轴,且函数f(x)在区间($\frac{π}{6}$,$\frac{2π}{3}$)上单调递减,则φ的值为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{5π}{6}$ | D. | $\frac{7π}{6}$ |