题目内容

　　求值:(1)a²sin(-1350º)+b²tan405º-(a-b)²cot765º-2abcos(-1080º)；

　　(2)tan+cot(-)-sin²()-.

答案：
解析：

　　分析:已知角求三角函数,可利用终边相同的同名三角函数值相等,这组诱导公式,将角化为[0º,360º)内的角,然后求解.

　　解:(1)原式=(-3×360º)

　　=a²sin90º+b²tan45º–(a-b)²cot45º-2abcos0º

　　=a²+b²-(a-b)²-2ab=0

　　(2)原式=

　　=

　　=

　　=.

　　评注：(1)运用公式一求任意角的三角函数值时，应先将角写成a+k·360º(k∈Z,0≤a＜360º=或a+2kp(k∈Z,0≤a＜2p的形式。

　　(2)熟记特殊角的三角函数值

练习册系列答案

课时天天练系列答案

课时学案系列答案

课堂达标100分系列答案

课堂过关循环练系列答案

课堂检测10分钟系列答案

课堂练习系列答案

课堂练习检测系列答案

课堂作业四点导学学案精编系列答案

课易通三维数字课堂系列答案

口算速算提优练习册系列答案

相关题目

若已知tan10°=a，求tan110°的值，那么在以下四个答案：①

中，正确的是（　　）

A、①和③	B、①和④
C、②和③	D、②和④

设(1+x+x2)n=a0+a1x+…+a2nx2n，求a₂+a₄+…+a_2n的值（　　）

（2013•黄浦区二模）已知数列{a_n}具有性质：①a₁为整数；②对于任意的正整数n，当a_n为偶数时，an+1=

；当a_n为奇数时，an+1=

．
（1）若a₁=64，求数列{a_n}的通项公式；
（2）若a₁，a₂，a₃成等差数列，求a₁的值；
（3）设a1=2m-3（m≥3且m∈N），数列{a_n}的前n项和为S_n，求证：Sn≤2m+1-m-5．（　　）

已知数列{a_n}的前n项和为S_n，且 $数学公式$ ，
（1）求a₁，a₂的值；　　　　　　　
（2）求数列{a_n}的通项a_n；
（3）设c_n=（3n+1）a_n，求数列{c_n}的前n项和T_n．

以下给出的是用条件语句编写的程序，根据该程序回答
READ　 x
IF　　 x＜a　　THEN　 y=-x²+ax+b
ELSEy=x²-ax+b
END　 IF
PRINT　 y
END
（Ⅰ）求证：输入x的值互为相反数则输出的y值也互为相反数的充要条件是a²+b²=0；
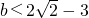（Ⅱ）设常数 $数学公式$ ，若在[0，1]随机输入x，则输出的y值为负，求实数a的取值范围．