题目内容
以下给出的是用条件语句编写的程序,根据该程序回答
READ x
IF x<a THEN y=-x2+ax+b
ELSEy=x2-ax+b
END IF
PRINT y
END
(Ⅰ) 求证:输入x的值互为相反数则输出的y值也互为相反数的充要条件是a2+b2=0;
(Ⅱ) 设常数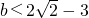 ,若在[0,1]随机输入x,则输出的y值为负,求实数a的取值范围.
,若在[0,1]随机输入x,则输出的y值为负,求实数a的取值范围.
解:(I)充分性:若a2+b2=0时,即a=b=0,所以f(x)=x|x|.∵f(-x)=-x|-x|=-x|x|=-f(x),对一切x∈R恒成立,∴f(x)是奇函数;
必要性:若f(x)是奇函数,则对一切x∈R,f(-x)=-f(x)恒成立,即-x|-x-a|+b=-x|x-a|-b.
令x=0,得b=-b,所以b=0.
再令x=a,得2a|a|=0,∴a=0,即a2+b2=0.
(II)∵ ,∴当x=0时,a取任意实数不等式恒成立,
,∴当x=0时,a取任意实数不等式恒成立,
故考虑 .∴
.∴
对(1)式,由b<0时,在 为增函数,∴
为增函数,∴ .∴a>1+b.(3)
.∴a>1+b.(3)
对(2)式,当 .
.
当 ,∴
,∴ .∴
.∴ .(4)
.(4)
由(3)、(4),要使a存在,必须有 .
.
∴当 .
.
当 为减函数,(证明略)
为减函数,(证明略)
综上所述,当 的取值范围是
的取值范围是 ;
;
当b<-1时,a的取值范围是(1+b,1-b).
分析:(I)充要条件的证明必须分清充分性与必要性.充分性是指若a2+b2=0时,判断f(x)是奇函数;必要性是由f(x)是奇函数,判断a2+b2=0;
(II)由于 ,故当x=0时,a取任意实数不等式恒成立,
,故当x=0时,a取任意实数不等式恒成立,
当 .所以只需对x∈(0,1],
.所以只需对x∈(0,1], (1),
(1), (2).下面只需要对(1)式,(2)式,分别研究即可得实数a的取值范围.
(2).下面只需要对(1)式,(2)式,分别研究即可得实数a的取值范围.
点评:本题的考点是必要条件、充分条件及充要条件的判断,主要考查充要性的证明,关键是读懂信息,搞清充分性与必要性,考查学生分析解决问题的能力,有一定的难度
必要性:若f(x)是奇函数,则对一切x∈R,f(-x)=-f(x)恒成立,即-x|-x-a|+b=-x|x-a|-b.
令x=0,得b=-b,所以b=0.
再令x=a,得2a|a|=0,∴a=0,即a2+b2=0.
(II)∵
 ,∴当x=0时,a取任意实数不等式恒成立,
,∴当x=0时,a取任意实数不等式恒成立,故考虑
 .∴
.∴
对(1)式,由b<0时,在
 为增函数,∴
为增函数,∴ .∴a>1+b.(3)
.∴a>1+b.(3)对(2)式,当
 .
.当
 ,∴
,∴ .∴
.∴ .(4)
.(4)由(3)、(4),要使a存在,必须有
 .
.∴当
 .
.当
 为减函数,(证明略)
为减函数,(证明略)
综上所述,当
 的取值范围是
的取值范围是 ;
;当b<-1时,a的取值范围是(1+b,1-b).
分析:(I)充要条件的证明必须分清充分性与必要性.充分性是指若a2+b2=0时,判断f(x)是奇函数;必要性是由f(x)是奇函数,判断a2+b2=0;
(II)由于
 ,故当x=0时,a取任意实数不等式恒成立,
,故当x=0时,a取任意实数不等式恒成立,当
 .所以只需对x∈(0,1],
.所以只需对x∈(0,1], (1),
(1), (2).下面只需要对(1)式,(2)式,分别研究即可得实数a的取值范围.
(2).下面只需要对(1)式,(2)式,分别研究即可得实数a的取值范围.点评:本题的考点是必要条件、充分条件及充要条件的判断,主要考查充要性的证明,关键是读懂信息,搞清充分性与必要性,考查学生分析解决问题的能力,有一定的难度

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
 以下给出的是用条件语句编写的一个程序,根据该程序回答:
以下给出的是用条件语句编写的一个程序,根据该程序回答:
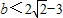 ,若在[0,1]随机输入x,则输出的y值为负,求实数a的取值范围.
,若在[0,1]随机输入x,则输出的y值为负,求实数a的取值范围.