题目内容
若已知tan10°=a,求tan110°的值,那么在以下四个答案:①
;②
;③
④
中,正确的是( )
a+
| ||
1-
|
a+
| ||
|
| a2-1 |
| 2a |
| 2 |
| 1-a2 |
| A、①和③ | B、①和④ |
| C、②和③ | D、②和④ |
分析:首先化简tan110°=tan(90°+20°)=-cot20°,然后分别用利用两角差正切公式和二倍角公式及诱导公式求出cot20°,
解答:解:tan110°=tan(90°+20°)=-cot20°
∵tan20°=tan(30°-10°)=
=
∴tan110°=tan(90°+20°)=-cot20°=
tan20°=
=
∵tan110°=tan(90°+20°)=-cot20°=
故选C.
∵tan20°=tan(30°-10°)=
| ||||
1+
|
| ||
3+
|
∴tan110°=tan(90°+20°)=-cot20°=
a+
| ||
|
tan20°=
| 2tan10° |
| 1-tan210 |
| 2a |
| 1-a2 |
∵tan110°=tan(90°+20°)=-cot20°=
| a2-1 |
| 2a |
故选C.
点评:本题考查了二倍角的正切和正切和差公式,解题中tan110°=tan(90°+20°)=-cot20°是关键,属于基础题.

练习册系列答案
 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
若已知tan10°=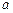 ,求tan110°的值,那么在以下四个答案:
,求tan110°的值,那么在以下四个答案:
①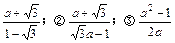 ④
④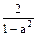 中,正确的是( )
中,正确的是( )
| A.①和③ | B.①和④ | C.②和③ | D.②和④ |
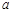 ,求tan110°的值,那么在以下四个答案:
,求tan110°的值,那么在以下四个答案: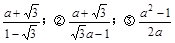 ④
④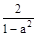 中,正确的是( )
中,正确的是( )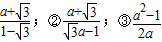 ④
④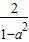 中,正确的是( )
中,正确的是( )