题目内容
已知a＞0，b＞0且
，求：
（1）a+b的最小值；
（2）若直线l与x轴、y轴分别交于A（a，0）、B（0，b），求VABO（O为坐标原点）面积的最小值．
解：∵
∴a+b=（a+b）×（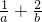
）=1+2+
≥3+2 
=3+2
当且仅当
时等号成立，
∴a+b的最小值为3+2
（2）∵
（4分）
则ab≥8（6分）
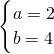取“=”，
∴△ABO（O为坐标原点）面积
ab的最小值4．…（12分）
分析：（1）根据 化简可以得到a+b=（a+b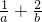）×（ ），再运用基本不等式可求得最小值．
（1）根据基本不等式的性质可知，进而求得△ABO（O为坐标原点）面积ab的最小值．
点评：本题主要考查基本不等式的应用．在基本不等式中要注意1的灵活运用，有时可以带来很大的方便．
∴a+b=（a+b）×（
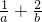）=1+2+≥3+2 =3+2当且仅当
时等号成立，∴a+b的最小值为3+2
（2）∵
（4分）则ab≥8（6分）
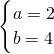取“=”，∴△ABO（O为坐标原点）面积
ab的最小值4．…（12分）分析：（1）根据
化简可以得到a+b=（a+b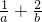）×（ ），再运用基本不等式可求得最小值．（1）根据基本不等式的性质可知
，进而求得△ABO（O为坐标原点）面积ab的最小值．点评：本题主要考查基本不等式的应用．在基本不等式中要注意1的灵活运用，有时可以带来很大的方便．
练习册系列答案
新编小学单元自测题系列答案
字词句段篇系列答案
相关题目
已知a＞0，b＞0且
+
=1，则a+2b的最小值为（ ）
| 1 |
| a |
| 3 |
| b |
A、7+2
| ||
B、2
| ||
C、7+2
| ||
| D、14 |