题目内容
设直线l的方程为x-y+1=0，则l关于直线x=2对称的直线l′的方程为（ ）
分析：根据关于直线x=2对称点的公式，将P（x，y）关于x=2对称的点坐标Q（4-x，y）代入直线l方程，即可求出直线l′的方程．
解答：解：∵点P（x，y）关于直线x=2对称的点坐标为Q（4-x，y）
∴直线l：x-y+1=0关于直线x=2对称的直线l′的方程为
l′：（4-x）-y+1=0，即x+y-5=0
故选：A
∴直线l：x-y+1=0关于直线x=2对称的直线l′的方程为
l′：（4-x）-y+1=0，即x+y-5=0
故选：A
点评：本题求直线l关于x=2对称的直线方程，着重考查了直线的方程与轴对称的有关公式等知识，属于基础题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
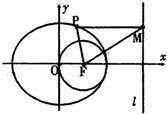如图，F是椭圆的右焦点，以F为圆心的圆过原点O和椭圆的右顶点，设P是椭圆的动点，P到两焦点距离之和等于4