题目内容
设直线l的方程为x+my-2m+6=0,根据下列条件分别确定m的值.
(1)直线l在x轴上的截距是-3;
(2)直线l的斜率是l.
(1)直线l在x轴上的截距是-3;
(2)直线l的斜率是l.
分析:(1)l在x轴上的截距是-3,即直线l过点(-3,0),代入方程,解之即可;
(2)由题意得斜率为1,即直线方程中x、y的系数互为相反数,且不为0,解方程求得实数m的值.
(2)由题意得斜率为1,即直线方程中x、y的系数互为相反数,且不为0,解方程求得实数m的值.
解答:解:(1)l在x轴上的截距是-3,即直线l过点(-3,0),
故-3+0-2m+6=0,
解得m=
;
(2)直线斜率为1,即直线方程中x、y的系数互为相反数,且不为0.
故1+m=0,解得m=-1.
故-3+0-2m+6=0,
解得m=
| 3 |
| 2 |
(2)直线斜率为1,即直线方程中x、y的系数互为相反数,且不为0.
故1+m=0,解得m=-1.
点评:本题考查直线的倾斜角和斜率的关系,以及解一元二次方程的方法,属于基础题.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
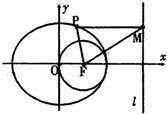 如图,F是椭圆的右焦点,以F为圆心的圆过原点O和椭圆的右顶点,设P是椭圆的动点,P到两焦点距离之和等于4
如图,F是椭圆的右焦点,以F为圆心的圆过原点O和椭圆的右顶点,设P是椭圆的动点,P到两焦点距离之和等于4