题目内容
（14分）叙述并证明余弦定理．
解：
叙述：余弦定理：三角形任何一边的平方等于其他两遍平方的和减去这两边与它们夹角的余
弦之积的两倍。或：在△ABC中，a，b，c为A，B，C的对边，有：
，
，
．
证明：（证法一） 如图，
即
同理可证，
（证法二）已知
中，
所对边分别为
，以
为原点，
所在直线为
轴建立直角坐标系，
则
，
∴
，
即
同理可证：，。
解析
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
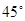方向,距离12 nmile的海面上有一走私船C正以10 nmile/h的速度沿东偏南
方向逃窜.缉私艇的速度为14 nmile/h, 若要在最短的时间内追上该走私船,缉私艇应沿北偏东
的方向去追,.求追及所需的时间和
角的正弦值.
中，
，
，
.
的值；（Ⅱ）求
的值.
的面积是30，
分别是三内角
的对边，且
.
； (2)若
，求
的值。
，
．已知
．
，求角A的大小；
，求
的取值范围．
的三个内角
所对的边分别为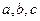
，向量
，
，且
.
的大小；
；②
；③
，试从中再选择两个条件以确定
，已知
.
，求角B的大小
、
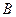两点的距离为
海里，
处，甲船自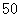
海里/小时的速度向
海里/小时的速度沿方位角
方向航行。问航行几小时两船之
间的距离最短？
与
的距离，由于地形的限制，需要在岸上选取
和
两点，现测得
，
，
，
，
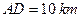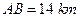，求两景点
