题目内容
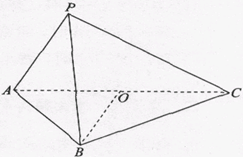
(本题12分)如图,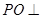 平面
平面 ,点
,点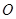 在
在 上,
上,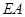 ∥
∥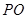 ,四边形
,四边形 为直角梯形,
为直角梯形,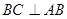 ,
, ,
,

(1)求证: 平面
平面 ;
;
(2)求二面角 的余弦值;
的余弦值;
(3)直线 上是否存在点
上是否存在点 ,使
,使 ∥平面
∥平面 ,若存在,求出点
,若存在,求出点 ;若不存在,说明理由。
;若不存在,说明理由。
(1)只需证 ;(2)
;(2) ;(3)存在M即为点E。
;(3)存在M即为点E。
解析试题分析:四边形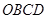 为正方形,所以
为正方形,所以 ,以OD为 x轴,OB为y轴,OP为z轴建立空间直角坐标系 …1分
,以OD为 x轴,OB为y轴,OP为z轴建立空间直角坐标系 …1分
(1)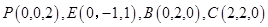 ,所以
,所以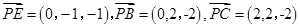 ,因为
,因为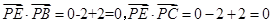 ,所以
,所以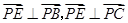 ,所以
,所以 平面
平面 …………4分
…………4分
(2)平面 的法向量为
的法向量为 ,平面
,平面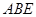 的法向量为
的法向量为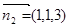
解得二面角的余弦值为 ……8分
……8分
(3)设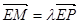 =
=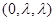 ,则
,则
由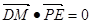 ,解得
,解得 ,存在M即为点E ……12分
,存在M即为点E ……12分
考点:线面垂直的判定定理;二面角;线面平行的判定定理。
点评:证明线面垂直的常用方法:
①线线垂直Þ线面垂直 若一条直线垂直平面内两条相交直线,则这条直线垂直这个平面。
若一条直线垂直平面内两条相交直线,则这条直线垂直这个平面。
即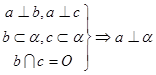
②面面垂直Þ线面垂直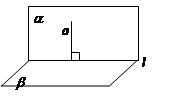 两平面垂直,其中一个平面内的一条直线垂直于它们的交线,则这条直线垂直于另一个平面。
两平面垂直,其中一个平面内的一条直线垂直于它们的交线,则这条直线垂直于另一个平面。
即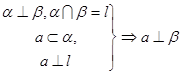
 ③两平面平行,有一条直线垂直于垂直于其中一个平面,则这条直线垂直于另一个平面。
③两平面平行,有一条直线垂直于垂直于其中一个平面,则这条直线垂直于另一个平面。
即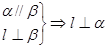
④两直线平行,其中一条直线垂直于这个平面,则另一条直线也垂直于这个平面。 即
即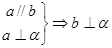
⑤向量法。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 中,
中,
 ,
,  ,D为AB中点。
,D为AB中点。
 ;
; ∥平面
∥平面 ;
;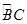 的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图).
的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图).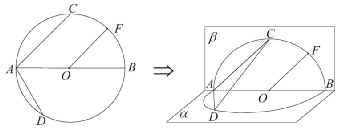
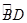 上是否存在点G,使得FG∥平面ACD?若存在,试指出点G的位置,并求直线AG与平面ACD所成角的正弦值;若不存在,请说明理由.
上是否存在点G,使得FG∥平面ACD?若存在,试指出点G的位置,并求直线AG与平面ACD所成角的正弦值;若不存在,请说明理由.

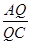 的值;若不存在,说明理由。
的值;若不存在,说明理由。 BCD=60
BCD=60 ,E是CD的中点,PA
,E是CD的中点,PA 底面ABCD,PA=2.
底面ABCD,PA=2.
 ,求AB1与C1B所成角的大小。
,求AB1与C1B所成角的大小。
