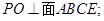题目内容
如图,⊙O的直径AB=4,点C、D为⊙O上两点,且∠CA B=45o,∠DAB=60o,F为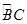 的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图).
的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图).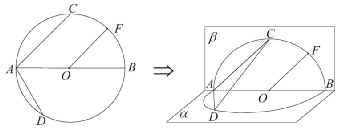
(1)求证:OF//平面ACD;
(2)求二面角C- AD-B的余弦值;
(3)在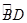 上是否存在点G,使得FG∥平面ACD?若存在,试指出点G的位置,并求直线AG与平面ACD所成角的正弦值;若不存在,请说明理由.
上是否存在点G,使得FG∥平面ACD?若存在,试指出点G的位置,并求直线AG与平面ACD所成角的正弦值;若不存在,请说明理由.
(1)只需证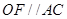 ;(2)
;(2)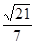 ;(3)
;(3)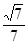 。
。
解析试题分析:(法一):证明:(1)如右图,连接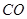 ,
, 
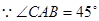 ,
,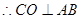 ,
,
又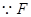 为
为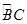 的中点,
的中点,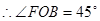 ,
,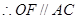 .
.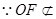 平面
平面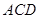 ,
,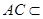 平面
平面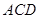 ,
,
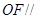 平面
平面 .3分
.3分
解:(2)过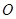 作
作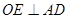 于
于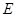 ,连
,连 .
. 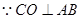 ,平面
,平面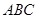 ⊥平面
⊥平面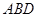 .
. 
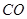 ⊥平面
⊥平面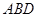 .
.
又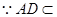 平面
平面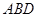 ,
, 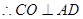 ,
, 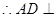 平面
平面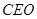 ,
,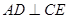 ,
,
则∠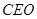 是二面角
是二面角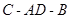 的平面角. 5分
的平面角. 5分
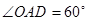 ,
,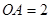 ,
, 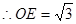 .
.
由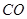 ⊥平面
⊥平面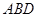 ,
,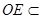 平面
平面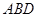 ,得
,得 为直角三角形,
为直角三角形,
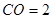 ,
,
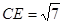 .
.
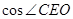 =
=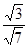 =
=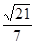 . 8分
. 8分
(3)设在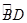 上存在点
上存在点 ,使得
,使得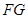 //平面
//平面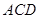 ,
,
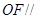 平面
平面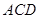 ,
,  平面
平面 平面
平面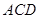 ,
,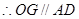 ,
,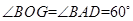 .
.
因此,在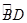 上存在点
上存在点 ,使得
,使得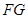 //平面
//平面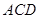 ,且点
,且点 为
为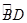 的中点.10分
的中点.10分
连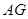 ,设
,设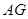 与平面
与平面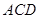 所成角为
所成角为

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
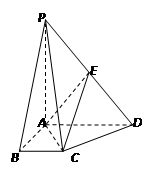
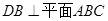 ,
,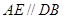 ,
,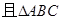 是边长为2的等边三角形,
是边长为2的等边三角形,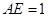 ,CD与平面ABDE所成角的正弦值为
,CD与平面ABDE所成角的正弦值为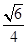 .
.
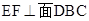 ,若存在,求线段DF的长度,若不存在,说明理由;
,若存在,求线段DF的长度,若不存在,说明理由;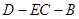 的平面角的余弦值.
的平面角的余弦值. BAD=90°,PA
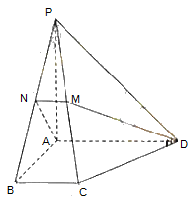
BAD=90°,PA 底面ABCD,且PA=AD=AB=2BC=2,M、N分别为PC、PB的中点.
底面ABCD,且PA=AD=AB=2BC=2,M、N分别为PC、PB的中点.
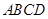 所在平面与平面四边形
所在平面与平面四边形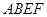 所在平面互相垂直,△
所在平面互相垂直,△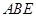 是等腰直角三角形,
是等腰直角三角形,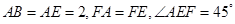
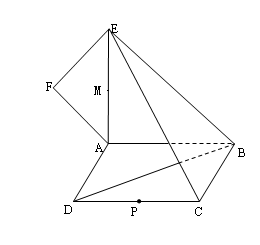
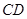 的中点为
的中点为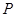 ,线段
,线段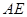 的中点为
的中点为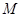 ,求证:
,求证: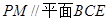 ;
;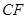 与平面
与平面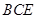 所成角的正切值.
所成角的正切值.
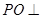 平面
平面 ,点
,点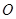 在
在 上,
上,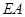 ∥
∥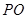 ,四边形
,四边形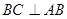 ,
, ,
,

 平面
平面 ;
; 的余弦值;
的余弦值; 上是否存在点
上是否存在点 ,使
,使 ∥平面
∥平面 中,
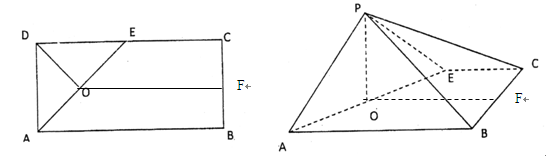
中, 的中点,F为BC的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且
的中点,F为BC的中点,O为AE的中点,以AE为折痕将△ADE向上折起,使D到P点位置,且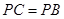 .
.