题目内容
已知函数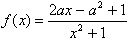 (x∈R),其中a∈R,
(x∈R),其中a∈R,
(Ⅰ)当a=1时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)当a≠0时,求函数f(x)的单调区间与极值。
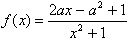 (x∈R),其中a∈R,
(x∈R),其中a∈R,(Ⅰ)当a=1时,求曲线y=f(x)在点(2,f(2))处的切线方程;
(Ⅱ)当a≠0时,求函数f(x)的单调区间与极值。
解:(Ⅰ)当a=1时,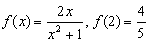 ,
,
又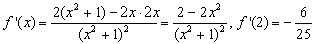 ,
,
所以,曲线y=f(x)在点(2,f(2))处的切线方程为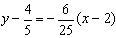 ,即6x+25y-32=0。
,即6x+25y-32=0。
(Ⅱ)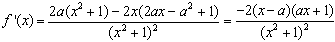 ,
,
由于a≠0,以下分两种情况讨论,
(1)当a>0时,令f′(x)=0,得到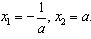 ,
,
当x变化时,f′(x),f(x)的变化情况如下表:
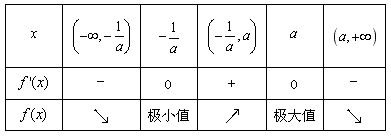
所以f(x)在区间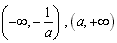 内为减函数,在区间
内为减函数,在区间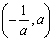 内为增函数,
内为增函数,
函数f(x)在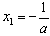 处取得极小值
处取得极小值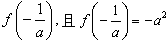 ;
;
函数f(x)在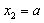 处取得极大值f(a),且f(a)=1;
处取得极大值f(a),且f(a)=1;
(2)当a<0时,令f′(x)=0,得到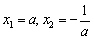 ,
,
当x变化时,f′(x),f(x)的变化情况如下表:
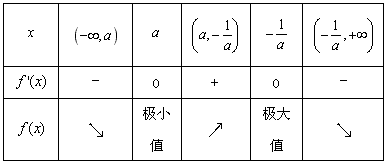
所以f(x)在区间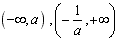 内为减函数,在区间
内为减函数,在区间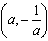 内为增函数,
内为增函数,
函数f(x)在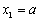 处取得极大值f(a),且f(a)=1;
处取得极大值f(a),且f(a)=1;
函数f(x)在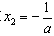 处取得极小值
处取得极小值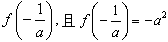 。
。
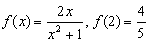 ,
,又
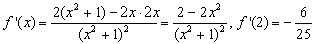 ,
,所以,曲线y=f(x)在点(2,f(2))处的切线方程为
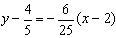 ,即6x+25y-32=0。
,即6x+25y-32=0。(Ⅱ)
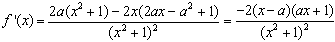 ,
,由于a≠0,以下分两种情况讨论,
(1)当a>0时,令f′(x)=0,得到
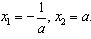 ,
,当x变化时,f′(x),f(x)的变化情况如下表:

所以f(x)在区间
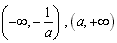 内为减函数,在区间
内为减函数,在区间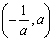 内为增函数,
内为增函数,函数f(x)在
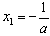 处取得极小值
处取得极小值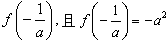 ;
;函数f(x)在
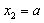 处取得极大值f(a),且f(a)=1;
处取得极大值f(a),且f(a)=1; (2)当a<0时,令f′(x)=0,得到
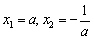 ,
,当x变化时,f′(x),f(x)的变化情况如下表:

所以f(x)在区间
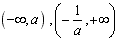 内为减函数,在区间
内为减函数,在区间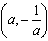 内为增函数,
内为增函数,函数f(x)在
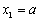 处取得极大值f(a),且f(a)=1;
处取得极大值f(a),且f(a)=1;函数f(x)在
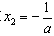 处取得极小值
处取得极小值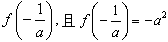 。
。 
练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
 (x∈R).若
(x∈R).若 ,
, .求cos2x的值.
.求cos2x的值. ,x∈R,且
,x∈R,且
 ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值.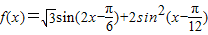 (x∈R).
(x∈R). ,x∈R
,x∈R
 ,x∈R,且
,x∈R,且
 ,
, ,
, ,求cos(α+β)的值.
,求cos(α+β)的值.