题目内容
设a≥b>0，求证：3a3＋2b3≥3a2b＋2ab2
证明 方法一3a3＋2b3－(3a2b＋2ab2)
＝3a2(a－b)＋2b2(b－a)＝(3a2－2b2)(a－b)．
因为a≥b>0，
所以a－b≥0,3a2－2b2>0，
从而(3a2－2b2)(a－b)≥0，
所以3a3＋2b3≥3a2b＋2ab2.
方法二 要证3a3＋2b3≥3a2b＋2ab2，
只需证3a2(a－b)－2b2(a－b)≥0，
只需证(3a2－2b2)(a－b)≥0，
∵a≥b>0.∴a－b≥0,3a2－2b2>2a2－2b2≥0，
∴上式成立．
练习册系列答案
相关题目
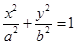=1（a,b>0）过M（2，
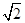），N(
,1)两点，O为坐标原点，
？若存在，写出该圆的方程，并求|AB |的取值范围，若不存在说明理由。
（a,b>0）过M（2，
） ，N(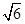
,1)两点，O为坐标原点．
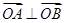？若存在，写出该圆的方程，若不存在说明理由。
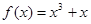，若a+b>0 , b+c>0 , c+a>0 , 则
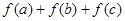的符号（ ）
（a,b>0）过M（2，
） ，N(
,1)两点，O为坐标原点，（I）求椭圆E的方程；
？若存在，写出该圆的方程，并求|AB |的取值范围，若不存在说明理由。