题目内容
19.如图6所示，等腰△ABC的底边AB=6
,高CD=3，点E是线段BD上异于点B、D的动点.点F在BC边上，且EF⊥AB.现沿EF将△BEF折起到△PEF的位置，使PE⊥AE.记 BE＝x，V(x)表示四棱锥P-ACFE的体积.
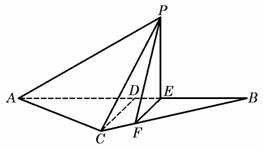
图6
（1）求V(x)的表达式；
（2）当x为何值时，V(x)取得最大值？
（3）当V(x)取得最大值时，求异面直线AC与PF所成角的余弦值
解：(1)已知EF
AB,那么翻折后，显然有PEEF,又PE
AE,从而PE
面ACFE,即PE为四棱锥的高。
四棱锥的底面积S=
-
而△BEF与△BDC相似，那么
=
=
=
则S=
-
=（1-
）
6
3=9
（1-
）
故四棱锥的体积V(x)=
Sh=
9
（1-
）
x =3
x（1-
）(0＜x＜3
)
(2) 
= 3
-
x2(0＜x＜3
)
令
=0得x=6
当x∈(0，6)时，
＞0,V(x)单调递增；x∈(6，3
)时，
＜0,V(x)单调递减；因此x=6时， V(x)取得最大值。V(x)max= V(6)=12
(3)
.
练习册系列答案
相关题目
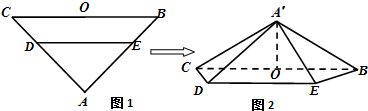如图1，在等腰△ABC中，∠A=90°，BC=6，D，E分别是AC，AB上的点，
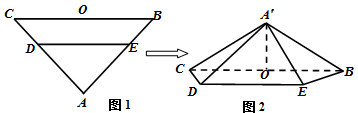
，O为BC的中点．将△ADE沿DE折起，得到如图(2)所示的四棱锥
，其中
．
平面BCDE；
的平面角的余弦值．
，O为BC的中点．将△ADE沿DE折起，得到如图2所示的四棱椎A′-BCDE，其中A′O=
．