题目内容
已知点(1, )是函数f(x)=ax(a>0且a≠1)的图象上一点,等比数列{an}的前n项和为f(n)-c,数列{bn}(bn>0)的首项为c,且前n项和Sn满足Sn-Sn-1=
)是函数f(x)=ax(a>0且a≠1)的图象上一点,等比数列{an}的前n项和为f(n)-c,数列{bn}(bn>0)的首项为c,且前n项和Sn满足Sn-Sn-1=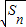 +
+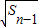 (n≥2).记数列{
(n≥2).记数列{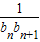 }前n项和为Tn,
}前n项和为Tn,(1)求数列{an}和{bn}的通项公式;
(2)若对任意正整数n,当m∈[-1,1]时,不等式t2-2mt+
 >Tn恒成立,求实数t的取值范围
>Tn恒成立,求实数t的取值范围(3)是否存在正整数m,n,且1<m<n,使得T1,Tm,Tn成等比数列?若存在,求出m,n的值,若不存在,说明理由.
【答案】分析:(1)因为点  是函数f(x)=ax的图象上一点,所以a=
是函数f(x)=ax的图象上一点,所以a= ,所以f(x)=
,所以f(x)= ,即可得到数列的前3项,进而求出数列的首项与公比,即可得到数列{an}的通项公式;
,即可得到数列的前3项,进而求出数列的首项与公比,即可得到数列{an}的通项公式;
因为 =
= ,所以数列{
,所以数列{  }是以1为首项,以1为公差的等差数列,所以得到Sn,利用bn=Sn-Sn-1求出答案.
}是以1为首项,以1为公差的等差数列,所以得到Sn,利用bn=Sn-Sn-1求出答案.
(2)利用裂项相消的方法可得:Tn= ;进而把原不等式化简为:当m∈[-1,1]时,不等式t2-2mt>0恒成立;设g(m)=-2tm+t2,m∈[-1,1],然后利用函数的有界性解决恒成立问题即可得到答案.
;进而把原不等式化简为:当m∈[-1,1]时,不等式t2-2mt>0恒成立;设g(m)=-2tm+t2,m∈[-1,1],然后利用函数的有界性解决恒成立问题即可得到答案.
(3)利用T1,Tm,Tn成等比数列,得Tm2=T1•Tn得到 ,
, ,最后结合1<m<n知,m=2,n=12即可.
,最后结合1<m<n知,m=2,n=12即可.
解答:解:(1)因为f(1)=a= ,所以f(x)=
,所以f(x)= ,
,
所以 ,a2=[f(2)-c]-[f(1)-c]=
,a2=[f(2)-c]-[f(1)-c]= ,a3=[f(3)-c]-[f(2)-c]=
,a3=[f(3)-c]-[f(2)-c]=
因为数列{an}是等比数列,所以 ,所以c=1.
,所以c=1.
又公比q= ,所以
,所以  ;
;
由题意可得: =
= ,
,
又因为bn>0,所以 ;
;
所以数列{ }是以1为首项,以1为公差的等差数列,并且有
}是以1为首项,以1为公差的等差数列,并且有  ;
;
当n≥2时,bn=Sn-Sn-1=2n-1;
所以bn=2n-1.
(2)因为数列 前n项和为Tn,
前n项和为Tn,
所以
=
= ;
;
因为当m∈[-1,1]时,不等式 恒成立,
恒成立,
所以只要当m∈[-1,1]时,不等式t2-2mt>0恒成立即可,
设g(m)=-2tm+t2,m∈[-1,1],
所以只要一次函数g(m)>0在m∈[-1,1]上恒成立即可,
所以 ,
,
解得t<-2或t>2,
所以实数t的取值范围为(-∞,-2)∪(2,+∞).
(3)T1,Tm,Tn成等比数列,得Tm2=T1•Tn
∴ ,
,
∴
结合1<m<n知,m=2,n=12(14分)
点评:本题综合考查数列、不等式与函数的有关知识,解决此类问题的关键是熟练掌握数列求通项公式与求和的方法,以及把不等式恒成立问题转化为函数求最值问题,然后利用函数的有关知识解决问题.
 是函数f(x)=ax的图象上一点,所以a=
是函数f(x)=ax的图象上一点,所以a= ,所以f(x)=
,所以f(x)= ,即可得到数列的前3项,进而求出数列的首项与公比,即可得到数列{an}的通项公式;
,即可得到数列的前3项,进而求出数列的首项与公比,即可得到数列{an}的通项公式;因为
 =
= ,所以数列{
,所以数列{  }是以1为首项,以1为公差的等差数列,所以得到Sn,利用bn=Sn-Sn-1求出答案.
}是以1为首项,以1为公差的等差数列,所以得到Sn,利用bn=Sn-Sn-1求出答案.(2)利用裂项相消的方法可得:Tn=
 ;进而把原不等式化简为:当m∈[-1,1]时,不等式t2-2mt>0恒成立;设g(m)=-2tm+t2,m∈[-1,1],然后利用函数的有界性解决恒成立问题即可得到答案.
;进而把原不等式化简为:当m∈[-1,1]时,不等式t2-2mt>0恒成立;设g(m)=-2tm+t2,m∈[-1,1],然后利用函数的有界性解决恒成立问题即可得到答案.(3)利用T1,Tm,Tn成等比数列,得Tm2=T1•Tn得到
 ,
, ,最后结合1<m<n知,m=2,n=12即可.
,最后结合1<m<n知,m=2,n=12即可.解答:解:(1)因为f(1)=a=
 ,所以f(x)=
,所以f(x)= ,
,所以
 ,a2=[f(2)-c]-[f(1)-c]=
,a2=[f(2)-c]-[f(1)-c]= ,a3=[f(3)-c]-[f(2)-c]=
,a3=[f(3)-c]-[f(2)-c]=
因为数列{an}是等比数列,所以
 ,所以c=1.
,所以c=1.又公比q=
 ,所以
,所以  ;
;由题意可得:
 =
= ,
,又因为bn>0,所以
 ;
;所以数列{
 }是以1为首项,以1为公差的等差数列,并且有
}是以1为首项,以1为公差的等差数列,并且有  ;
;当n≥2时,bn=Sn-Sn-1=2n-1;
所以bn=2n-1.
(2)因为数列
 前n项和为Tn,
前n项和为Tn,所以

=

=
 ;
;因为当m∈[-1,1]时,不等式
 恒成立,
恒成立,所以只要当m∈[-1,1]时,不等式t2-2mt>0恒成立即可,
设g(m)=-2tm+t2,m∈[-1,1],
所以只要一次函数g(m)>0在m∈[-1,1]上恒成立即可,
所以
 ,
,解得t<-2或t>2,
所以实数t的取值范围为(-∞,-2)∪(2,+∞).
(3)T1,Tm,Tn成等比数列,得Tm2=T1•Tn
∴
 ,
,∴

结合1<m<n知,m=2,n=12(14分)
点评:本题综合考查数列、不等式与函数的有关知识,解决此类问题的关键是熟练掌握数列求通项公式与求和的方法,以及把不等式恒成立问题转化为函数求最值问题,然后利用函数的有关知识解决问题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 )是函数
)是函数 且
且 )的图象上一点,等比数列
)的图象上一点,等比数列 的前
的前 项和为
项和为 ,数列
,数列
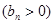 的首项为
的首项为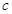 ,且前
,且前 满足
满足 =
= +
+ (
( ).
). 前
前 .
. )是函数f(x)=ax(a>0),且a≠1)的图象上一点,等比数列{an}的前n项和为f(n)-c,数列{bn}(bn>0)的首项为c,且前n项和Sn满足Sn-Sn-1=
)是函数f(x)=ax(a>0),且a≠1)的图象上一点,等比数列{an}的前n项和为f(n)-c,数列{bn}(bn>0)的首项为c,且前n项和Sn满足Sn-Sn-1= +
+ (n≥2).
(n≥2). }前n项和为Tn,问Tn>
}前n项和为Tn,问Tn> 的最小正整数n是多少?
的最小正整数n是多少? )是函数f(x)=ax(a>0),且a≠1)的图象上一点,等比数列{an}的前n项和为f(n)-c,数列{bn}(bn>0)的首项为c,且前n项和Sn满足Sn-Sn-1=
)是函数f(x)=ax(a>0),且a≠1)的图象上一点,等比数列{an}的前n项和为f(n)-c,数列{bn}(bn>0)的首项为c,且前n项和Sn满足Sn-Sn-1= +
+ (n≥2).
(n≥2). }前n项和为Tn,问Tn>
}前n项和为Tn,问Tn> 的最小正整数n是多少?
的最小正整数n是多少? )是函数
)是函数 且
且 )的图象上一点,等比数列
)的图象上一点,等比数列 的前
的前 项和为
项和为 ,数列
,数列
 的首项为
的首项为 ,且前
,且前 满足
满足 =
= +
+ (
(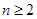 ).
). 前
前 ,问
,问 的最小正整数
的最小正整数